Chapter 7: Cellular Automata

Kente cloth (photo by ZSM)

Originating from the Akan people of Ghana, kente cloth is a woven fabric celebrated for its vibrant colors and intricate patterns. Woven in narrow strips, each design is unique, and when joined, the strips form a tapestry of complex and emergent patterns that tell a story or carry a message. The image shows three typical Ewe kente stripes, highlighting the diverse weaving traditions that reflect the rich cultural tapestry of Ghana.

---

In Chapter 5, I defined a complex system as a network of elements with short-range relationships, operating in parallel, that exhibit emergent behavior. I created a flocking simulation to demonstrate how a complex system adds up to more than the sum of its parts. In this chapter, I’m going to turn to developing other complex systems known as cellular automata.

In some respects, this shift may seem like a step backward. No longer will the individual elements of my systems be members of a physics world, driven by forces and vectors to move around the canvas. Instead, I’ll build systems out of the simplest digital element possible: a single bit. This bit is called a cell, and its value (0 or 1) is called its state. Working with such simple elements will help reveal how complex systems operate, and will offer an opportunity to elaborate on some programming techniques that apply to code-based projects. Building cellular automata will also set the stage for the rest of the book, where I’ll increasingly focus on systems and algorithms rather than vectors and motion—albeit systems and algorithms that I can and will apply to moving bodies.

What Is a Cellular Automaton?

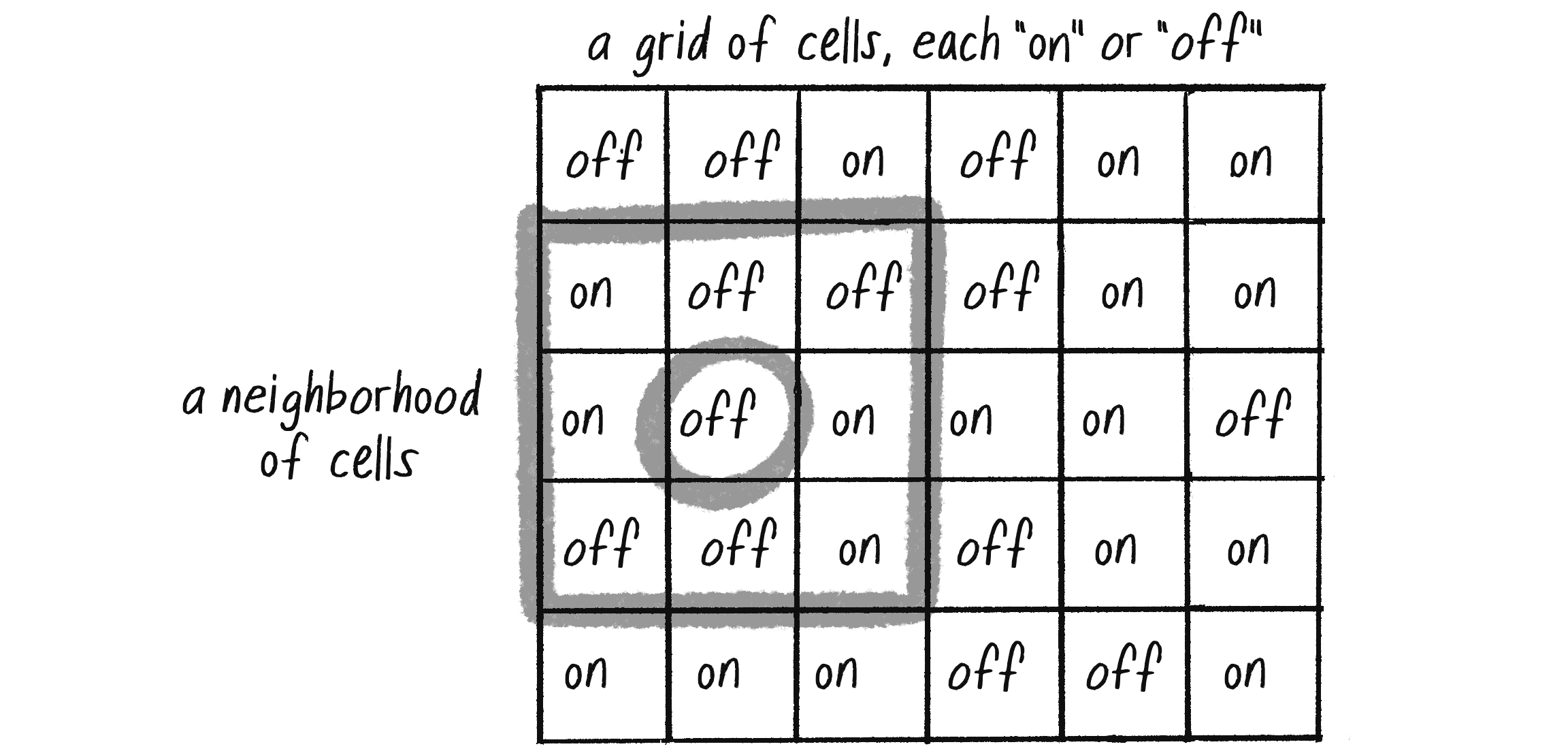
A cellular automaton (cellular automata plural, or CA for short) is a model of a system of cell objects with the following characteristics:

• The cells live on a grid. (I’ll include examples in both one and two dimensions in this chapter, though a CA can exist in any finite number of dimensions.)
• Each cell has a state, though a cell’s state can vary over time. The number of possible states is typically finite. The simplest example has the two possibilities of 1 and 0 (otherwise referred to as on and off, or alive and dead).
• Each cell has a neighborhood. This can be defined in any number of ways, but it’s typically all the cells adjacent to that cell.

It’s important to stress that the cells in a CA don’t refer to biological cells (although you’ll see how CA can mimic lifelike behavior and have applications in biology). Instead, they simply represent discrete units in a grid, similar to the cells in a spreadsheet (as in Microsoft Excel). Figure 7.1 illustrates a CA and its various characteristics.

The second CA feature I listed—the idea that a cell’s state can vary over time—is an important new development. So far in this book, the objects (movers, particles, vehicles, boids, bodies) have generally existed in only one state. They might have moved with sophisticated behaviors and physics, but ultimately they remained the same type of object over the course of their digital lifetime. I’ve alluded to the possibility that these entities can change over time (for example, the weights of steering “desires” can vary), but I haven’t fully put this into practice. Now, with CA, you’ll see how an object’s state can change based on a system of rules.

The development of CA systems is typically attributed to Stanisław Ulam and John von Neumann, who were both researchers at the Los Alamos National Laboratory in New Mexico in the 1940s. Ulam was studying the growth of crystals, and von Neumann was imagining a world of self-replicating robots. You read that right: robots that can build copies of themselves.

Von Neumann’s original cells had 29 possible states, so perhaps the idea of self-replicating robots is a bit too complex of a starting point. Instead, imagine a row of dominoes; each domino can be in one of two states: standing upright (1) or knocked down (0). Just as dominoes react to their neighboring dominoes, the behavior of each cell in a CA is influenced by the states of its neighboring cells.

This chapter explores how even the most basic rules of something like dominoes can lead to a wide array of intricate patterns and behaviors, similar to natural processes like biological reproduction and evolution. Von Neumann’s work in self-replication and CA is conceptually similar to what’s probably the most famous CA, the Game of Life, which I’ll discuss in detail later in the chapter.

Perhaps the most significant (and lengthy) scientific work studying CA arrived in 2002: Stephen Wolfram’s 1,280-page A New Kind of Science. Available in its entirety for free online, Wolfram’s book discusses how CA aren’t simply neat tricks but are relevant to the study of biology, chemistry, physics, and all branches of science. In a moment, I’ll turn to building a simulation of Wolfram’s work, although I’ll barely scratch the surface of the theories he outlines—my focus will be on the code implementation, not the philosophical implications. If the examples spark your curiosity, you’ll find plenty more to read about in Wolfram’s book, as well as in his ongoing research at the Wolfram Physics Project.

Elementary Cellular Automata

What’s the simplest CA you can imagine? For Wolfram, an elementary CA has three key elements:

• Grid
• States
• Neighborhood

The simplest grid would be 1D: a line of cells (Figure 7.2).

The simplest set of states (beyond having only one state) would be two states: 0 or 1 (Figure 7.3). Perhaps the initial states are set randomly.

The simplest neighborhood in one dimension for any given cell would be the cell itself and its two adjacent neighbors: one to the left and one to the right (Figure 7.4). I’ll have to decide what I want to do with the cells on the left and right edges, since those have only one neighbor each, but I can sort out this detail later.

I have a line of cells, each with an initial state, and each with two neighbors. The exciting thing is, even with this simplest CA imaginable, the properties of complex systems can emerge. But I haven’t yet discussed perhaps the most important detail of how CA work: change over time.

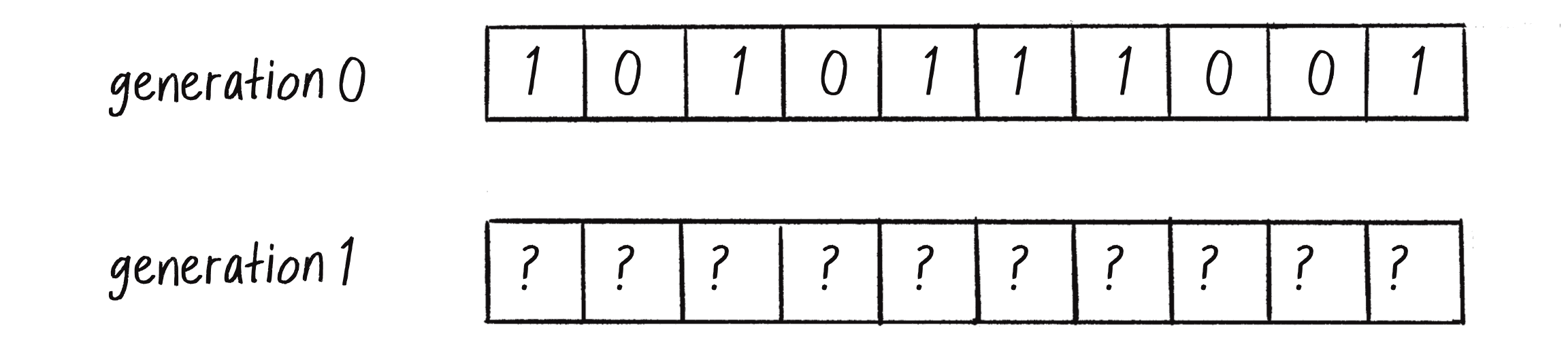
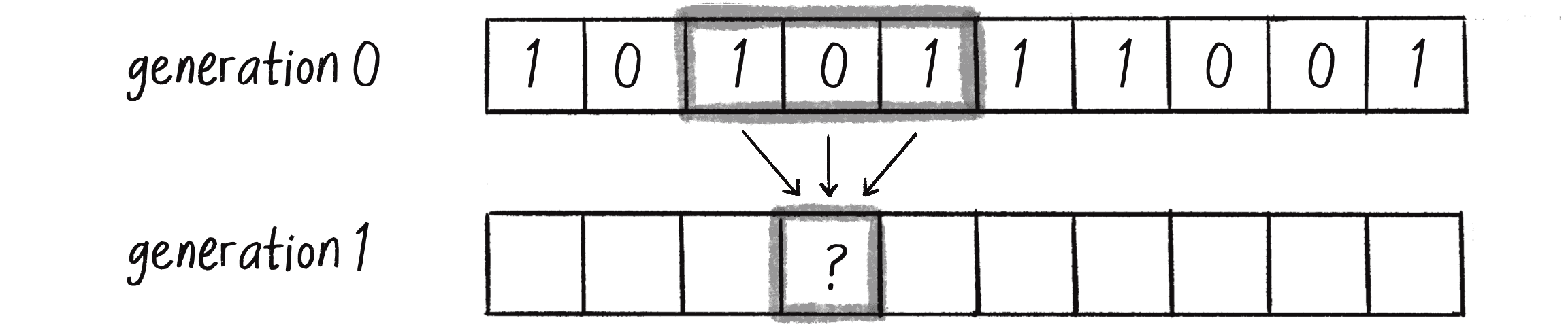
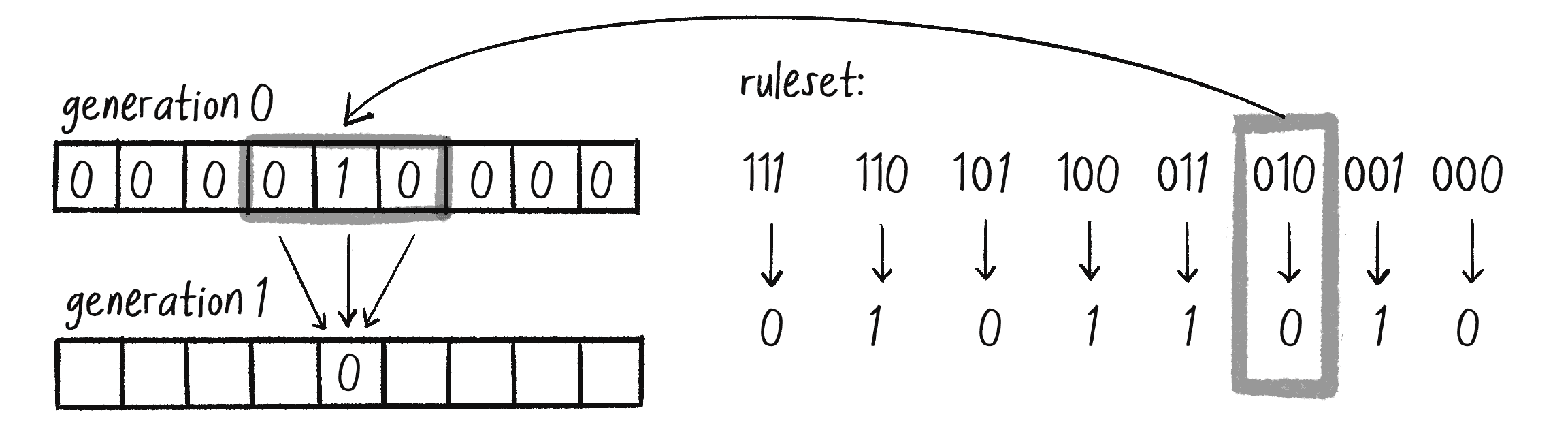
I’m not talking about real-world time here, but rather about the CA developing across a series of discrete time steps, which could also be called generations. In the case of a CA in p5.js, time will likely be tied to the frame count of the animation. The question, as depicted in Figure 7.5, is this: Given the states of the cells at time equals 0 (or generation 0), how do I compute the states for all cells at generation 1? And then how do I get from generation 1 to generation 2? And so on and so forth.

Let’s say that the CA has an individual cell called $\text{cell}$. The formula for calculating the cell’s state at any given time $t$ ($\text{cell}_t$) is as follows:

In other words, a cell’s new state is a function of all the states in the cell’s neighborhood at the previous generation (time $t-1$). A new state value is calculated by looking at the previous generation’s neighbor states (Figure 7.6).

You can compute a cell’s state from its neighbors’ states in many ways. Consider blurring an image. (Guess what? Image processing works with CA-like rules!) A pixel’s new state (its color) is the average of its neighbors’ colors. Similarly, a cell’s new state could be the sum of all its neighbors’ states. However, in Wolfram’s elementary CA, the process takes a different approach: instead of mathematical operations, new states are determined by predefined rules that account for every possible configuration of a cell and its neighbors. These rules are known collectively as a ruleset.

This approach might seem ridiculous at first—wouldn’t there be way too many possibilities for it to be practical? Well, let’s give it a try. A neighborhood consists of three cells, each with a state of 0 or 1. How many possible ways can the states in a neighborhood be configured? A quick way to figure this out is to think of each neighborhood configuration as a binary number. Binary numbers use base 2, meaning they’re represented with only two possible digits (0 and 1). In this case, each neighborhood configuration corresponds to a 3-bit number, and how many values can you represent with 3 bits? Eight, from 0 (000) up to 7 (111). Figure 7.7 shows how.

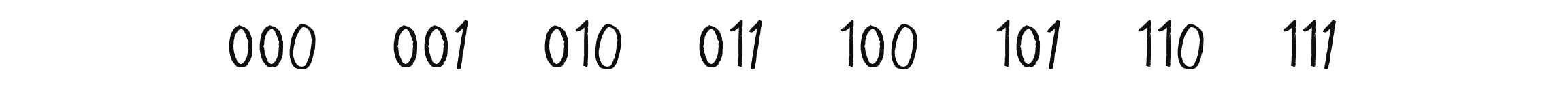
Once all the possible neighborhood configurations are defined, an outcome (new state value: 0 or 1) is specified for each configuration. In Wolfram’s original notation and other common references, these configurations are written in descending order. Figure 7.8 follows this convention, starting with 111 and counting down to 000.

Keep in mind that unlike the sum or averaging method, the rulesets in elementary CA don’t follow any arithmetic logic—they’re just arbitrary mappings of inputs to outputs. The input is the current configuration of the neighborhood (one of eight possibilities), and the output is the next state of the middle cell in the neighborhood (0 or 1—it’s up to you to define the rule).

Once you have a ruleset, you can set the CA in motion. The standard Wolfram model is to start generation 0 with all cells having a state of 0 except for the middle cell, which should have a state of 1. You can do this with any size (length) grid, but for clarity, I’ll use a 1D CA of nine cells so that the middle is easy to pick out (see Figure 7.9).

Based on the ruleset in Figure 7.8, how do the cells change from generation 0 to generation 1? Figure 7.10 shows how the center cell, with a neighborhood of 010, switches from a 1 to a 0. Try applying the ruleset to the remaining cells to fill in the rest of the generation 1 states.

Now for a slight change: instead of representing the cells’ states with 0s and 1s, I’ll indicate them with visual cues—white for 0 and black for 1 (see Figure 7.11). Although this might seem counterintuitive, as 0 usually signifies black in computer graphics, I’m using this convention because the examples in this book have a white background, so “turning on” a cell corresponds to switching its color from white to black.

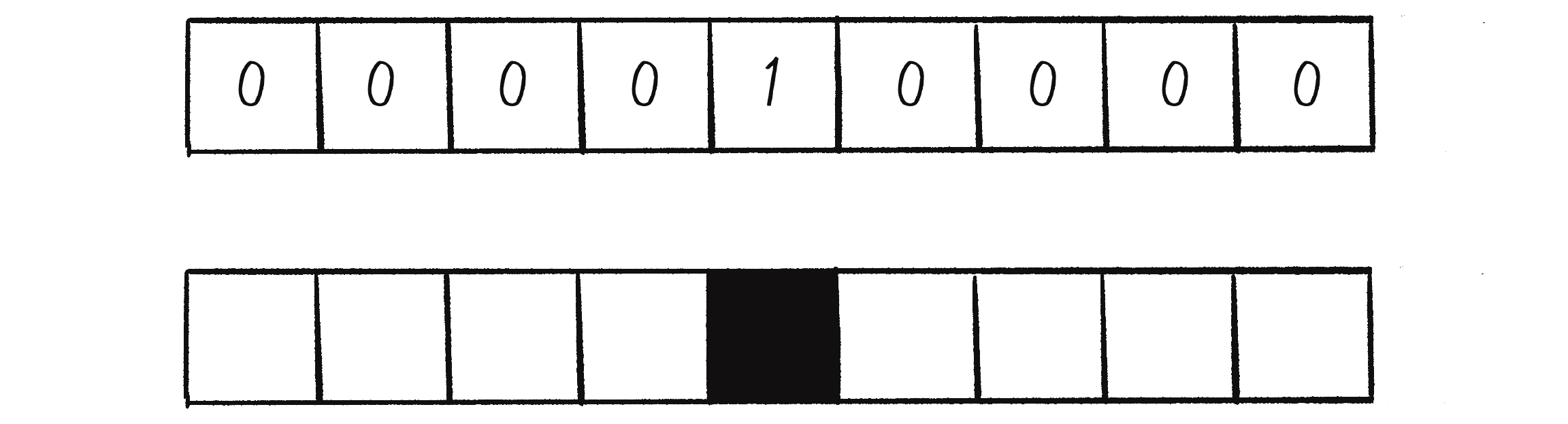
With this switch from numerical representations to visual forms, the fascinating dynamics and patterns of CA will come into view! To show them even more clearly, instead of drawing one generation at a time, I’ll also start stacking the generations, with each new generation appearing below the previous one, as shown in Figure 7.12.

The low-resolution shape that emerges in Figure 7.12 is the Sierpiński triangle. Named after the Polish mathematician Wacław Sierpiński, it’s a famous example of a fractal. I’ll examine fractals more closely in Chapter 8, but briefly, they’re patterns in which the same shapes repeat themselves at different scales. To give you a better sense of this, Figure 7.13 shows the CA over several more generations and with a wider grid size.

And Figure 7.14 shows the CA again, this time with cells that are just a single pixel wide so the resolution is much higher.

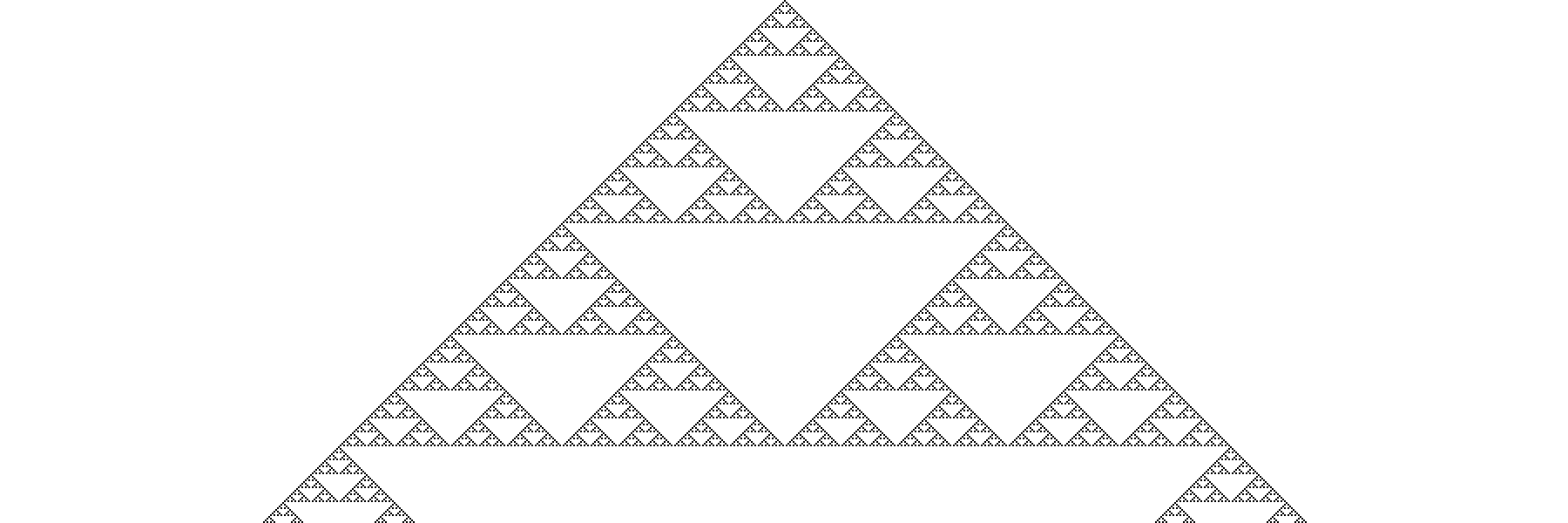
Take a moment to let the enormity of what you’ve just seen sink in. Using an incredibly simple system of 0s and 1s, with little neighborhoods of three cells, I was able to generate a shape as sophisticated and detailed as the Sierpiński triangle. This is the beauty of complex systems.

Of course, this particular result didn’t happen by accident. I picked the set of rules in Figure 7.8 because I knew the pattern it would generate. The mere act of defining a ruleset doesn’t guarantee visually exciting results. In fact, for a 1D CA in which each cell can have two possible states, there are exactly 256 possible rulesets to choose from, and only a handful are on par with the Sierpiński triangle. How do I know there are 256 possible rulesets? It comes down to a little more binary math.

Defining Rulesets

Take a look back at Figure 7.7 and notice again the eight possible neighborhood configurations, from 000 to 111. These are a ruleset’s inputs, and they remain constant from ruleset to ruleset. Only the outputs vary from one ruleset to another—the individual 0 or 1 paired with each neighborhood configuration. Figure 7.8 represented a ruleset entirely with 0s and 1s. Now Figure 7.15 shows the same ruleset visualized with white and black squares.

Since the eight possible inputs are the same no matter what, potential shorthand for indicating a ruleset is to specify just the outputs, writing them as a sequence of eight 0s or 1s—in other words, an 8-bit binary number. For example, the ruleset in Figure 7.15 could be written as 01011010. The 0 on the right corresponds to input configuration 000, the 1 next to it corresponds to input 001, and so on. On Wolfram’s website, CA rules are illustrated using a combination of this binary shorthand and the black-and-white square representation, yielding depictions like Figure 7.16.

I’ve said that each ruleset can essentially be boiled down to an 8-bit number, and how many combinations of eight 0s and 1s are there? Exactly $2^8$, or 256. You might remember this from when you first learned about RGB color in p5.js. When you write background(r, g, b), each color component (red, green, and blue) is represented by an 8-bit number ranging from 0 to 255 in decimal, or 00000000 to 11111111 in binary.

The ruleset in Figure 7.16 could be called rule 01011010, but Wolfram instead refers to it as rule 90. Where does 90 come from? To make ruleset naming even more concise, Wolfram uses decimal (or base 10) representations rather than binary. To name a rule, you convert its 8-bit binary number to its decimal counterpart. The binary number 01011010 translates to the decimal number 90, and therefore it’s named rule 90.

Since there are 256 possible combinations of eight 0s and 1s, there are also 256 unique rulesets. Let’s check out another one. How about rule 11011110, or more commonly, rule 222? Figure 7.17 shows how it looks.

The result is a recognizable shape, though it certainly isn’t as exciting as the Sierpiński triangle. As I said earlier, most of the 256 elementary rulesets don’t produce compelling outcomes. However, it’s still quite incredible that even just a few of these rulesets—simple systems of cells with only two possible states—can produce fascinating patterns seen every day in nature. For example, Figure 7.18 shows a snail shell resembling Wolfram’s rule 30. This demonstrates how valuable CAs can be in simulation and pattern generation.

Before I go too far down the road of characterizing the results of different rulesets, though, let’s look at how to build a p5.js sketch that generates and visualizes a Wolfram elementary CA.

Programming an Elementary CA

You may be thinking, “Okay, I have this cell thing. And the cell thing has properties, like a state, what generation it’s on, who its neighbors are, and where it lives pixel-wise on the screen. And maybe it has functions, like to display itself and determine its new state.” This line of thinking is an excellent one and would likely lead you to write code like this:

class Cell {

}

However, this isn’t the road I want to travel down right now. Later in this chapter, I’ll discuss why an object-oriented approach could prove valuable in developing a CA simulation, but to begin, it’s easier to work with a more elementary data structure. After all, what is an elementary CA but a list of 0s and 1s? Why not describe a generation of a 1D CA by using an array?

let cells = [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0];

This array corresponds to the row of cells shown in Figure 7.19.

To show that array, I check whether each element is a 0 or a 1, choose a fill color accordingly, and draw a rectangle:

for (let i = 0; i < cells.length; i++) {

  if (cells[i] === 0) {
    fill(255);
  } else {
    fill(0);
  }

  stroke(0);

  rect(i * 50, 0, 50, 50);

}

The array describes the cell states in the current generation. Now I need a mechanism to compute the next generation’s states. Here’s the pseudocode describing what I want to achieve:

For every cell in the array:

1. Take a look at the neighborhood states: left, middle, right.
2. Look up the new value for the cell state according to a ruleset.
3. Set the cell’s state to that new value.

This pseudocode may suggest writing code like this:

for (let i = 0; i < cells.length; i++) {

  let left   = cells[i - 1];
  let middle = cells[i];
  let right  = cells[i + 1];

  let newstate = rules(left, middle, right);

  cells[i] = newstate;

}

I’m fairly close to getting this right but have a few issues to resolve. For one, I’m farming out the calculation of a new state value to a function called rules(). Obviously, I’m going to have to write this function, so my work isn’t done, but what I’m aiming for here is modularity. I want a for loop that provides a basic framework for managing any CA, regardless of the specific ruleset. If I want to try different rulesets, I shouldn’t have to touch that framework at all; I can just rewrite the rules() function to compute the new states differently.

So I still have the rules() function to write, but more important, I’ve made one minor blunder and one major blunder in the for loop. Let’s examine the code more closely.

First, notice how easy it is to look at a cell’s neighbors. Because an array is an ordered list of data, I can use the numbering of the indices to know which cells are next to which cells. I know that cell number 15, for example, has cell 14 to its left and 16 to its right. More generally, I can say that for any cell i, its neighbors are i - 1 and i + 1.

In fact, it’s not quite that easy. What have I done wrong? Think about how the code will execute. The first time through the loop, cell index i equals 0. The code wants to look at cell 0’s neighbors. Left is i - 1 or -1. Oops! An array by definition doesn’t have an element with an index of -1. It starts with index 0!

I alluded to this problem of edge cases earlier in the chapter and said I could worry about it later. Well, later is now. How should I handle the cell on the edge that doesn’t have a neighbor to both its left and its right? Here are three possible solutions to this problem:

1. Edges remain constant. This is perhaps the simplest solution. Don’t bother to evaluate the edges, and always leave their state value constant (0 or 1).
2. Edges wrap around. Think of the CA as a strip of paper, and turn that strip of paper into a ring. The cell on the left edge is a neighbor of the cell on the right edge, and vice versa. This can create the appearance of an infinite grid and is probably the most commonly used solution.
3. Edges have different neighborhoods and rules. If I wanted to, I could treat the edge cells differently and create rules for cells that have a neighborhood of two instead of three. You may want to do this in some circumstances, but in this case, it’s going to be a lot of extra lines of code for little benefit.

To make the code easiest to read and understand right now, I’ll go with option 1 and skip the edge cases, leaving the values constant. This can be accomplished by starting the loop one cell later and ending it one cell earlier:

for (let i = 1; i < cells.length - 1; i++) {
  let left   = cells[i - 1];
  let middle = cells[i];
  let right  = cells[i + 1];
  let newstate = rules(left, middle, right);
  cells[i] = newstate;
}

I need to fix one more problem before this is done, and identifying it is absolutely fundamental to the techniques behind programming CA simulations. The bug is subtle and won’t trigger an error; the CA just won’t perform correctly. It all lies in this line of code:

  cells[i] = newstate;

This may seem perfectly innocent. After all, once I’ve computed a new state value, I want to assign the cell its new state. But think about the next iteration of the for loop. Let’s say the new state for cell 5 was just computed, and the loop is moving on to cell 6. What happens next?

Cell 6, generation 1 = a function of states for cell 5, cell 6, and cell 7 at generation 0

A cell’s new state is a function of the previous neighbor states, so in this case, the value of cell 5 at generation 0 is needed in order to calculate cell 6’s new state at generation 1. Have I saved cell 5’s value at generation 0? No! Remember, this line of code was just executed for i equals 5:

  cells[i] = newstate;

Once this happens, cell 5’s state at generation 0 is gone; cells[5] is now storing the value for generation 1. I can’t overwrite the values in the array while I’m processing the array, because I need those values to calculate the new values!

A solution to this problem is to have two arrays, one to store the current generation’s states and one for the next generation’s states. To save myself the step of reinitializing an array, I’ll use JavaScript’s slice() array method, which makes a copy of an array:

let newcells = cells.slice();

for (let i = 1; i < cells.length - 1; i++) {

  let left   = cells[i - 1];
  let middle = cells[i];
  let right  = cells[i + 1];

  let newstate = rules(left, middle, right);

  newcells[i] = newstate;

}

Once the current generation’s array of values has been completely processed, the cells variable can be assigned the new array of states, effectively throwing away the previous generation’s values:

cells = newcells;

I’m almost done, but I still need to define rules(), the function that computes the new state value based on the neighborhood (left, middle, and right cells). I know the function needs to return an integer (0 or 1), as well as receive three arguments (for the three neighbors):

  function rules(a, b, c) { return _______ }

I could write this function in many ways, but I’d like to start with a long-winded one that will hopefully provide a clear illustration of what’s happening. How shall I store the ruleset? Remember that a ruleset is a series of 8 bits (0 or 1) that define the outcome for every possible neighborhood configuration. If you need a refresher, Figure 7.20 shows the Wolfram notation for the Sierpiński triangle ruleset, along with the corresponding 0s and 1s listed in order. This should give you a hint as to the data structure I have in mind!

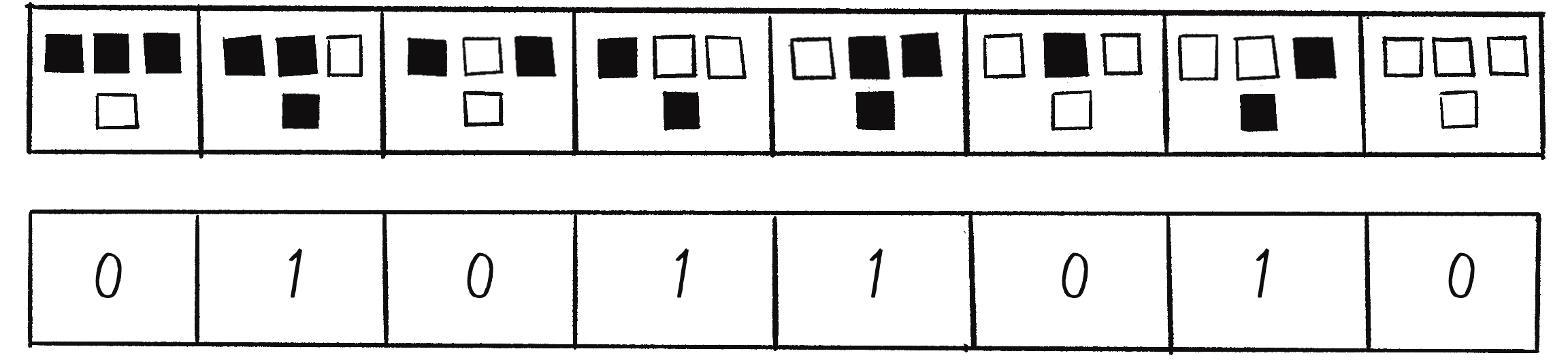
I can store this ruleset in an array:

let ruleset = [0, 1, 0, 1, 1, 0, 1, 0];

And then I can say, for example, this:

if (a === 1 && b === 1 && c === 1) return ruleset[0];

If left, middle, and right all have the state 1, that matches the configuration 111, so the new state should be equal to the first value in the ruleset array. Duplicating this strategy for all eight possibilities looks like this:

  function rules(a, b, c) {

    if      (a === 1 && b === 1 && c === 1) return ruleset[0];

    else if (a === 1 && b === 1 && c === 0) return ruleset[1];

    else if (a === 1 && b === 0 && c === 1) return ruleset[2];

    else if (a === 1 && b === 0 && c === 0) return ruleset[3];

    else if (a === 0 && b === 1 && c === 1) return ruleset[4];

    else if (a === 0 && b === 1 && c === 0) return ruleset[5];

    else if (a === 0 && b === 0 && c === 1) return ruleset[6];

    else if (a === 0 && b === 0 && c === 0) return ruleset[7];

  }

I like writing the rules() function this way because it describes line by line exactly what’s happening for each neighborhood configuration. However, it’s not a great solution. After all, what if a CA has
four possible states (0 through 3) instead of two? Suddenly there are 64 possible neighborhood configurations. And with 10 possible states, 1,000 configurations. And just imagine programming von Neumann’s 29 possible states. I’d be stuck typing out thousands upon thousands of else...if statements!

Another solution, though not quite as transparent, is to convert the neighborhood configuration (a 3-bit number) into a regular integer and use that value as the index into the ruleset array. This can be done as follows, using JavaScript’s built-in parseInt() function:

  function rules(a, b, c) {

    let s = "" + a + b + c;

    let index = parseInt(s, 2);

    return ruleset[index];

  }

This solution has one tiny problem, however. Consider rule 222:

let ruleset = [1, 1, 0, 1, 1, 1, 1, 0];

And say the neighborhood being tested is 111. The resulting state should be equal to ruleset index 0, based on the way I first wrote the rules() function:

  if (a === 1 && b === 1 && c === 1) return ruleset[0];

The binary number 111 converts to the decimal number 7. But I don’t want ruleset[7]; I want ruleset[0]. For this to work, I need to invert the index before looking up the state in the ruleset array:

  return ruleset[7 - index];

I now have everything needed to compute the generations for a Wolfram elementary CA. Here’s how the code looks all together:

let cells = [];

let ruleset = [0, 1, 0, 1, 1, 0, 1, 0];

function setup() {

  for (let i = 0; i < width; i++) {
    cells[i] = 0;
  }

  cells[floor(cells.length / 2)] = 1;

}

function draw() {

  let nextgen = cells.slice();
  for (let i = 1; i < cells.length - 1; i++) {
    let left = cells[i - 1];
    let me = cells[i];
    let right = cells[i + 1];
    nextgen[i] = rules(left, me, right);
  }

  cells = nextgen;

}

function rules(a, b, c) {
  let s = "" + a + b + c;
  let index = parseInt(s, 2);
  return ruleset[7 - index];
}

This is great, but one more piece is still missing: What good is a CA if you can’t see it?

Drawing an Elementary CA

The standard technique for drawing an elementary CA is to stack the generations one on top of
the other, and to draw each cell as a square that’s black (for state 1) or white (for state 0), as in Figure 7.21. Before implementing this particular visualization, however, I’d like to point out two things.

First, this visual interpretation of the data is completely literal. It’s useful for demonstrating the algorithms and results of Wolfram’s elementary CA, but it shouldn’t necessarily drive your own personal work. You’re not likely building a project that needs precisely this algorithm with this visual style. So, while learning to draw a CA in this way will help you understand and implement CA systems, this skill should exist only as a foundation.

Second, the fact that a 1D CA is visualized with a 2D image can be misleading. It’s very important to remember that this is not a 2D CA. I’m simply choosing to show a history of all the generations stacked vertically. This technique creates a 2D image out of many instances of 1D data, but the system itself is 1D. Later, I’ll show you an actual 2D CA (the Game of Life), and I’ll cover how to visualize such a system.

The good news is that drawing an elementary CA isn’t particularly difficult. I’ll begin by rendering a single generation. Let’s say each cell should be a 10$\times$10 square:

let w = 10;

Assuming the canvas is 640 pixels wide, the CA will have 64 cells. Of course, I can calculate this value dynamically when I initialize the cells array in setup():

let cells = new Array(floor(width / w));

Drawing the cells now involves iterating over the array and drawing a square based on the state of each cell:

for (let i = 0; i < cells.length; i++) {

  fill(cells[i] * 255);

  square(i * w, 0, w);

}

Two aspects of this code are off. First, when multiplying the state by 255, cells with a state of 1 will be white and those with 0 will be black, which is the opposite of what I originally intended! While this is of course okay since the color representation is arbitrary, I’ll correct this in the full example.

The more pressing issue is that the y-position for each square is hardcoded to 0. If I want the generations to be stacked on top of each other, with each row of cells marking a new generation, I’ll also need to calculate a y-position based on the generation number. I can accomplish this by adding a generation variable and incrementing it each time through draw(). With these additions, I can now look at the entire sketch.

let cells;

let generation = 0;

let w = 10;

let ruleset = [0, 1, 0, 1, 1, 0, 1, 0];

function setup() {

  createCanvas(640, 240);

  background(255);

  cells = new Array(floor(width / w));
  for (let i = 0; i < cells.length; i++) {
    cells[i] = 0;
  }
  cells[floor(cells.length / 2)] = 1;

}

function draw() {

  for (let i = 1; i < cells.length - 1; i++) {

    if (cells[i] === 1) {

      fill(0);

      square(i * w, generation * w, w);

    }

  }

  let nextgen = cells.slice();
  for (let i = 1; i < cells.length - 1; i++) {
    let left = cells[i - 1];
    let me = cells[i];
    let right = cells[i + 1];
    nextgen[i] = rules(left, me, right);
  }

  cells = nextgen;

  generation++;

}

function rules(a, b, c) {
  let s = "" + a + b + c;
  let index = parseInt(s, 2);
  return ruleset[7 - index];
}

You may have noticed an optimization I made in this example to simplify the drawing: I included a white background and rendered only the black squares, which saves the work of drawing many squares. This solution isn’t suitable for all cases—what if I want multicolored cells?—but it provides a performance boost in this simple case. (I’ll also note that if the size of each cell were 1 pixel, I wouldn’t want to use p5.js’s square() function, but rather access the pixel array directly.)

Despite this optimization, another aspect of the drawing code is woefully inefficient: the sketch continues to draw generation after generation, extending beyond the bottom of the canvas. The code on the book’s website includes a simple stopping condition, but you might come up with other approaches to address this issue (some are mentioned in the following exercises).

Wolfram Classification

Now that you have a sketch for visualizing an elementary CA, you can supply it whatever ruleset you want and see the results. What kinds of outcomes can you expect? As I noted earlier, the vast majority of elementary CA rulesets produce visually uninspiring results, while some result in wondrously complex patterns like those found in nature. Wolfram has divided the range of outcomes into four classes.

Class 1: Uniformity

Class 1 CAs end up, after a certain number of generations, with every cell constant. This isn’t terribly exciting to watch. Rule 222 is a class 1 CA; if you run it for enough generations, every cell will eventually become and remain black (see Figure 7.22).

Class 2: Repetition

Like class 1 CAs, class 2 CAs remain stable, but the cell states aren’t constant. Instead, they oscillate in a repeating pattern of 0s and 1s. In rule 190, each cell follows the sequence 11101110111011101110 (Figure 7.23).

Class 3: Random

Class 3 CAs appear random and have no easily discernible pattern. In fact, rule 30 (Figure 7.24) is used as a random-number generator in Wolfram’s Mathematica software. Again, you can feel amazed that such a simple system with simple rules can descend into a chaotic and random pattern.

Class 4: Complexity

Class 4 CAs can be thought of as a mix between class 2 and class 3. You can find repetitive, oscillating patterns inside the CA, but where and when these patterns appear is unpredictable and seemingly random. If a class 3 CA wowed you, then a class 4 like rule 110 (Figure 7.25) should really blow your mind!

In Chapter 5, I introduced the concept of a complex system and used flocking to demonstrate how simple rules can result in emergent behaviors. Class 4 CAs remarkably exhibit the characteristics of complex systems and are the key to simulating phenomena such as forest fires, traffic patterns, and the spread of diseases. Research and applications of CA consistently emphasize the importance of class 4 as the bridge between CA and nature.

The Game of Life

The next step is to move from a 1D CA to a 2D one: the Game of Life. This will introduce additional complexity—each cell will have a bigger neighborhood—but with the complexity comes a wider
range of possible applications. After all, most of what happens in computer graphics lives in two dimensions, and this chapter demonstrates how to apply CA thinking to a 2D p5.js canvas.

In 1970, Martin Gardner wrote a Scientific American article that documented mathematician John Conway’s new Game of Life, describing it as recreational mathematics: “To play life you must have a fairly large checkerboard and a plentiful supply of flat counters of two colors. It is possible to work with pencil and graph paper but it is much easier, particularly for beginners, to use counters and a board.”

The Game of Life has become something of a computational cliché, as myriad projects display the game on LEDs, screens, projection surfaces, and so on. But practicing building the system with code is still valuable for a few reasons.

For one, the Game of Life provides a good opportunity to practice skills with 2D arrays, nested loops, and more. Perhaps more important, however, this CA’s core principles are tied directly to a core goal of this book: simulating the natural world with code. The Game of Life algorithm and technical implementation will provide you with the inspiration and foundation to build simulations that exhibit the characteristics and behaviors of biological systems of reproduction.

Unlike von Neumann, who created an extraordinarily complex system of states and rules, Conway wanted to achieve a similar lifelike result with the simplest set of rules possible. Let’s look at how Gardner outlined Conway’s goals.

1. There should be no initial pattern for which there is a simple proof that the population can grow without limit.
2. There should be initial patterns that apparently do grow without limit.
3. There should be simple initial patterns that grow and change for a considerable period of time before coming to an end in three possible ways: fading away completely (from overcrowding or becoming too sparse), settling into a stable configuration that remains unchanged thereafter, or entering an oscillating phase in which they repeat an endless cycle of two or more periods.

This might sound cryptic, but it essentially describes a Wolfram class 4 CA. The CA should be patterned but unpredictable over time, eventually settling into a uniform or oscillating state. In other words, though Conway didn’t use this terminology, the Game of Life should have all the properties of a complex system.

The Rules of the Game

Let’s look at how the Game of Life works. It won’t take up too much time or space, since I can build on everything from Wolfram’s elementary CA. First, instead of a line of cells, I now have a 2D matrix of cells. As with the elementary CA, the possible states are 0 or 1. In this case, however, since the system is all about life, 0 means “dead” and 1 means “alive.”

Since the Game of Life is 2D, each cell’s neighborhood has now expanded. If a neighbor is an adjacent cell, a neighborhood is now nine cells instead of three, as shown in Figure 7.26.

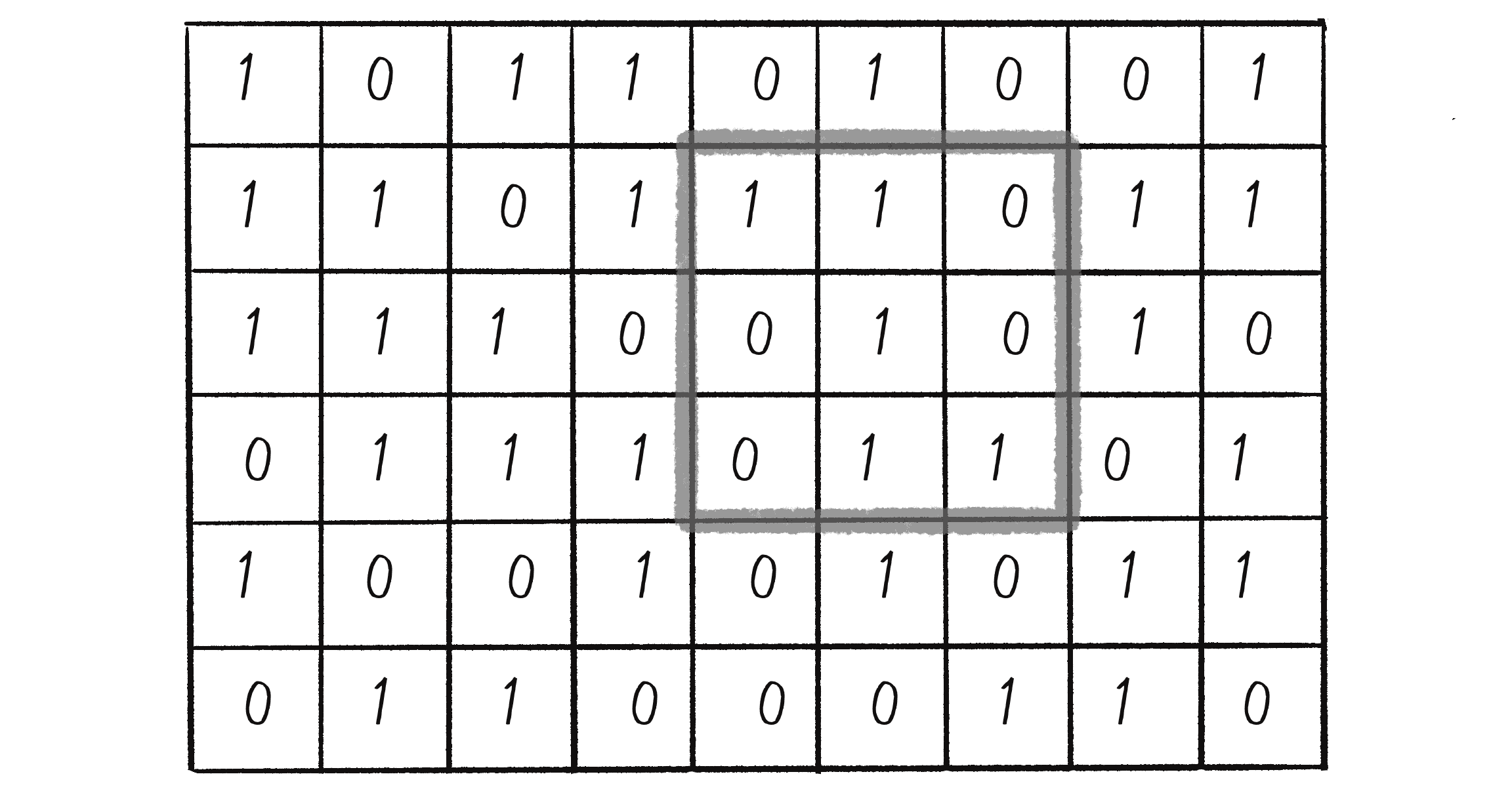
With three cells, a 3-bit number had eight possible configurations. With nine cells, there are 9 bits, or 512 possible neighborhoods. In most cases, defining an outcome for every single possibility would be impractical. The Game of Life gets around this problem by defining a set of rules according to general characteristics of the neighborhood: Is the neighborhood overpopulated with life, surrounded by death, or just right? Here are the rules of life:

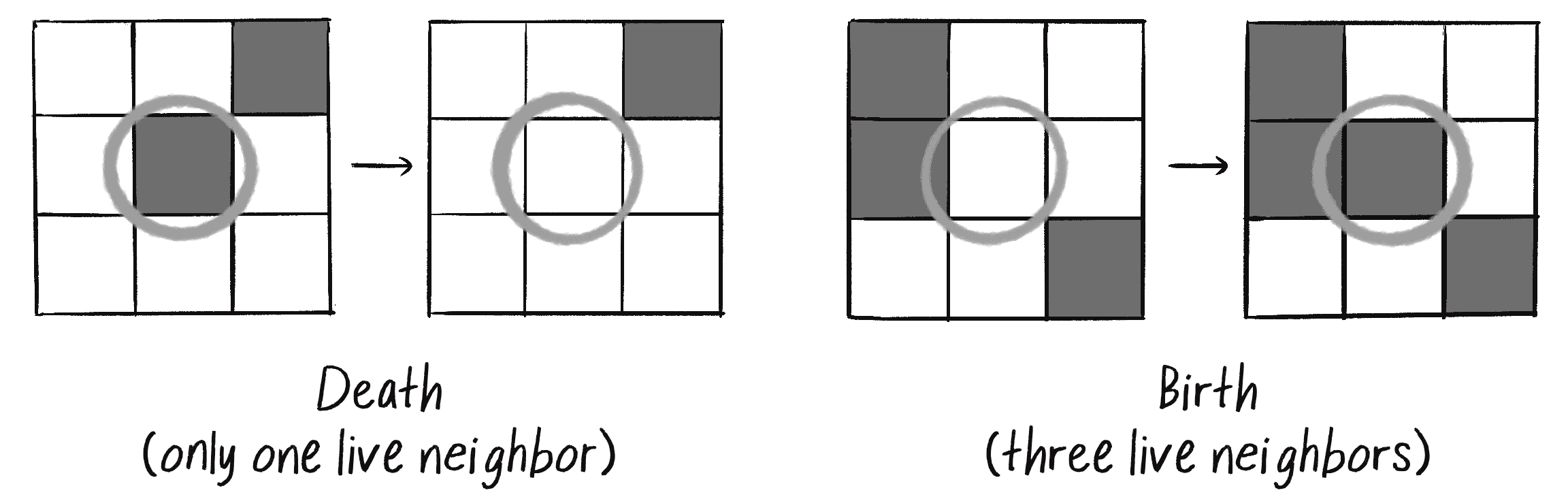
1. Death: If a cell is alive (state = 1), it will die (state becomes 0) under the following circumstances:
   • Overpopulation: If the cell has four or more living neighbors, it dies.
   • Loneliness: If the cell has one or fewer living neighbors, it dies.
2. Birth: If a cell is dead (state = 0), it will come to life (state becomes 1) when it has exactly three living neighbors (no more, no less).
3. Stasis: In all other cases, the cell’s state doesn’t change. Two scenarios are possible:
   • Staying alive: If a cell is alive and has exactly two or three live neighbors, it stays alive.
   • Staying dead: If a cell is dead and has anything other than three live neighbors, it stays dead.

Figure 7.27 shows a few examples of these rules. Focus on what happens to the center cell.

With the elementary CA, I visualized many generations at once, stacked as rows in a 2D grid. With the Game of Life, however, the CA is in two dimensions. I could try to create an elaborate 3D visualization of the results and stack all the generations in a cube structure (and in fact, you might want to try this as an exercise), but a more typical way to visualize the Game of Life is to treat each generation as a single frame in an animation. This way, instead of viewing all the generations at once, you see them one at a time, and the result resembles rapidly developing bacteria in a petri dish.

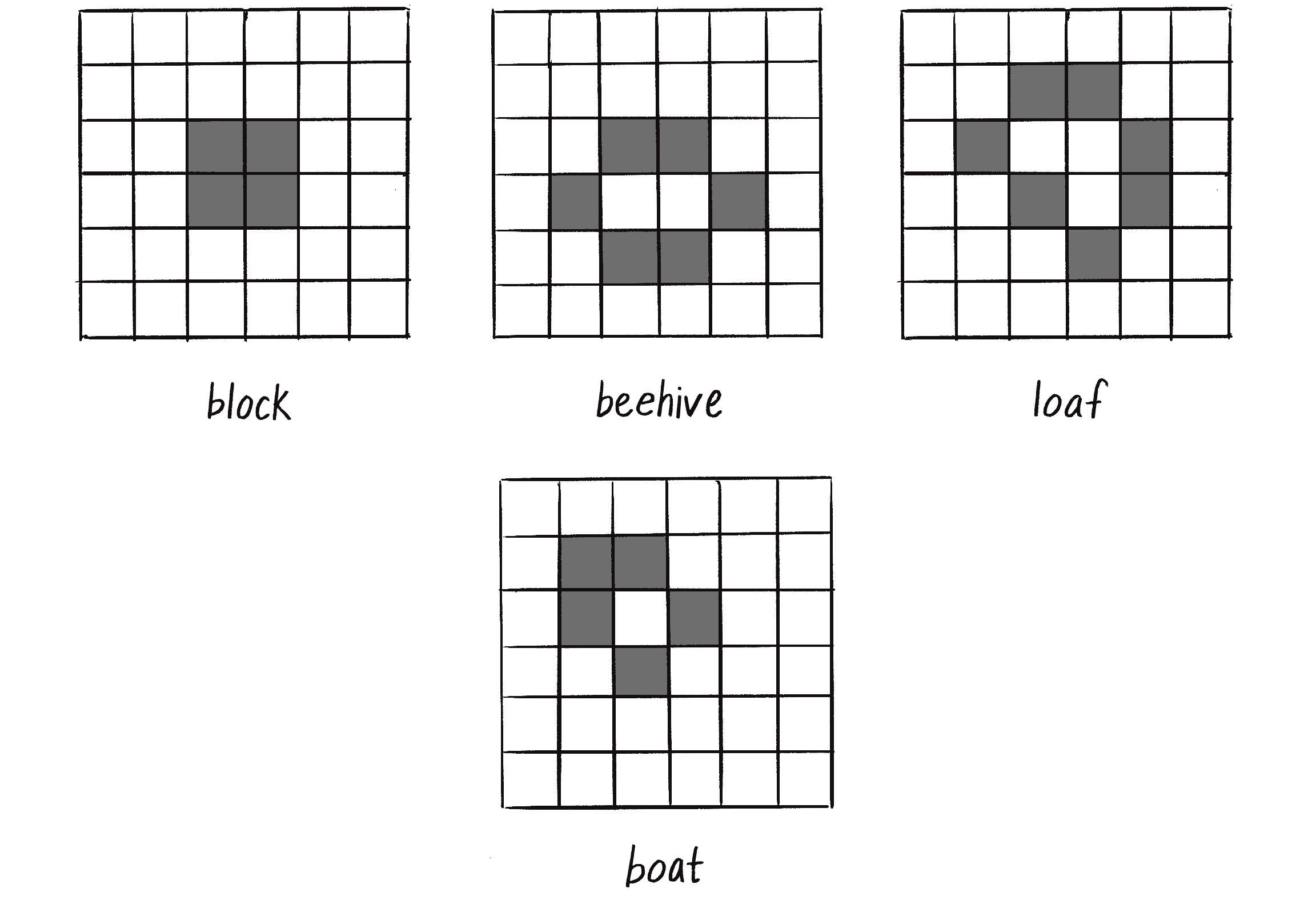
One of the exciting aspects of the Game of Life is that some known initial patterns yield intriguing results. For example, the patterns shown in Figure 7.28 remain static and never change.

The patterns in Figure 7.29 oscillate back and forth between two states.

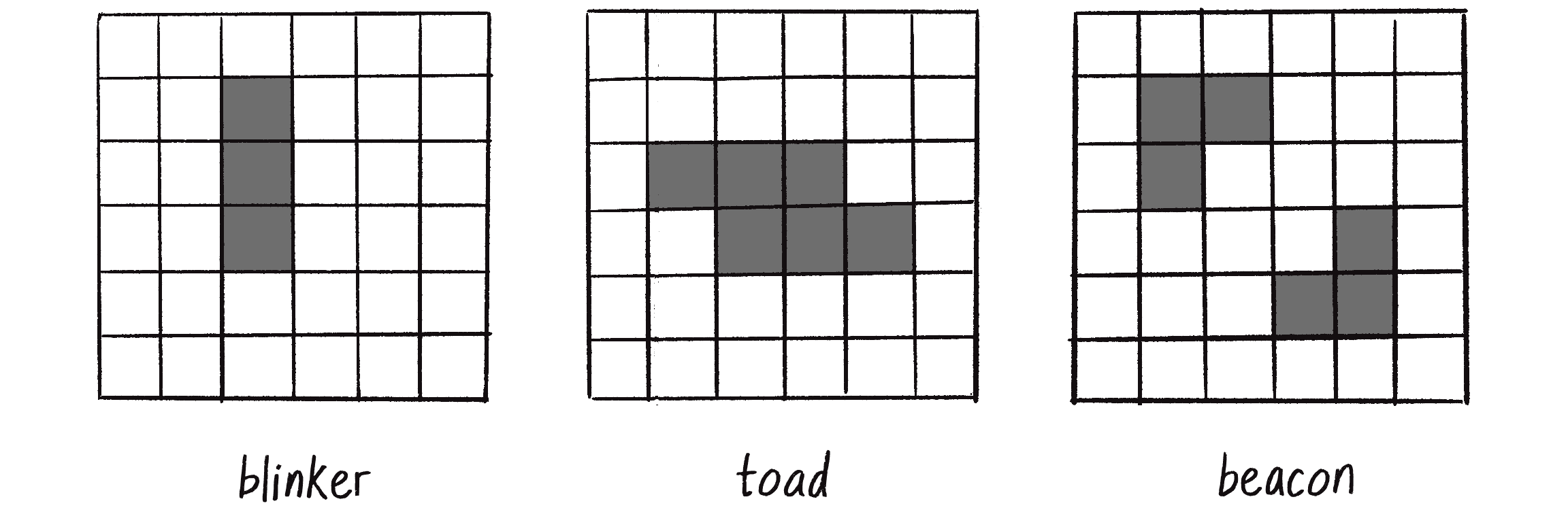
And the patterns in Figure 7.30 appear to move about the grid from generation to generation. The cells themselves don’t actually move, but you see the illusion of motion in the result of adjacent cells turning on and off.

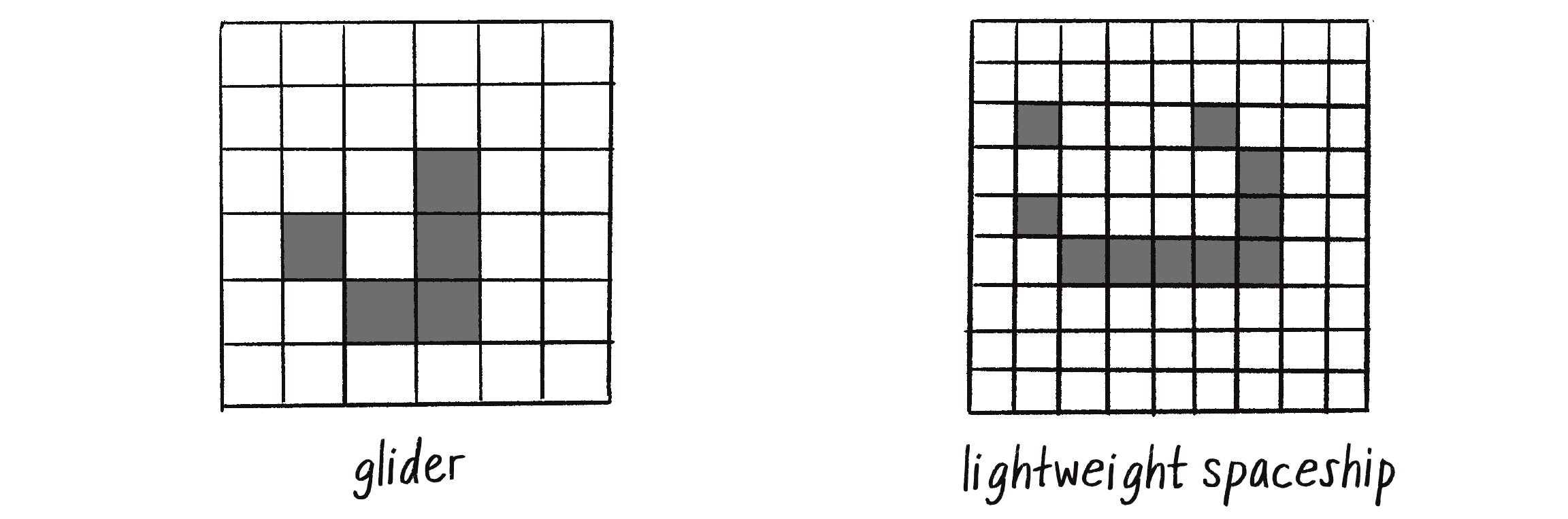
If you’re interested in these patterns, several good out-of-the-box Game of Life online demonstrations allow you to configure the CA’s initial state and watch it run at varying speeds. Here are two examples:

• Exploring Emergence by Mitchel Resnick and Brian Silverman, Lifelong Kindergarten Group, MIT Media Laboratory
• Conway’s Game of Life in p5.js by Steven Klise

For the example I’ll build in the next section, I’ll focus on randomly initializing the states for each cell.

The Implementation

I already have a lot of what I need to implement the Game of Life in p5.js: mostly, I just need to extend the code from the Wolfram CA sketch to two dimensions. I previously used a 1D array to store the list of cell states. Now I’ll use a 2D array:

let w = 8;

let columns = width / w;

let rows = height / w;

let board = new Array(columns);

for (let i = 0; i < columns; i++) {

  board[i] = new Array(rows);

}

I’ll begin by initializing each cell of the board with a random state, 0 or 1:

for (let i = 0; i < columns; i++) {

  for (let j = 0; j < rows; j++) {

    board[i][j] = floor(random(2));

  }

}

Just as before, I need an extra 2D array to receive the next generation’s states so I don’t overwrite the current generation’s 2D array as I’m processing it. Rather than write all the steps to create a 2D array in both setup() and draw(), however, it’s worth writing a function that returns a 2D array based on the number of columns and rows. I’ll also initialize each element of the array to 0 so that it isn’t filled with undefined:

function create2DArray(columns, rows) {

  let arr = new Array(columns);

  for (let i = 0; i < columns; i++) {

    arr[i] = new Array(rows);

    for (let j = 0; j < rows; j++) {

      arr[i][j] = 0;

    }

  }

  return arr;

}

Now I can just call that function whenever a new 2D array is required:

let next = create2DArray(columns, rows);

for (let i = 0; i < columns; i++) {

  for (let j = 0; j < rows; j++) {

    next[x][y] = _______________?;

  }

}

Next, I need to sort out how to calculate each cell’s new state. For that, I need to determine how to reference the cell’s neighbors. In the case of a 1D CA, this was simple: if a cell index was i, its neighbors were i-1 and i+1. Here, each cell doesn’t have a single index, but rather a column and row index: i,j. As shown in Figure 7.31, the neighbors are i-1,j-1 , i,j-1, i+1,j-1, i-1,j, i+1,j, i-1,j+1, i,j+1, and i+1,j+1.

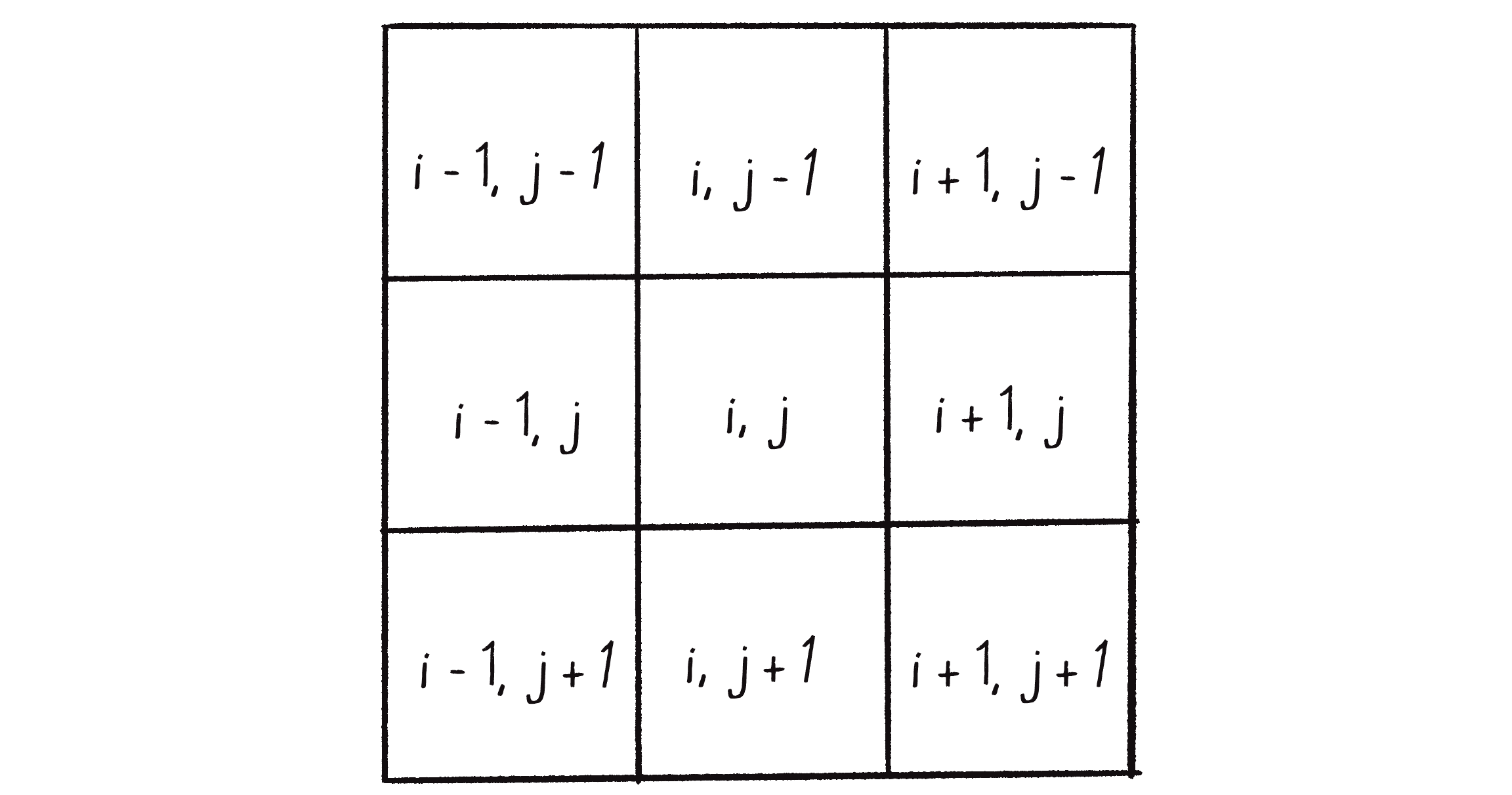
The Game of Life rules operate by knowing how many neighbors are alive. If I create a variable neighborSum and increment it for each neighbor with a state of 1, I’ll have the total of live neighbors:

let neighborSum = 0;

if (board[i - 1][j - 1] === 1) neighborSum++;
if (board[i    ][j - 1] === 1) neighborSum++;
if (board[i + 1][j - 1] === 1) neighborSum++;

if (board[i - 1][j    ] === 1) neighborSum++;
if (board[i + 1][j    ] === 1) neighborSum++;

if (board[i - 1][j + 1] === 1) neighborSum++;
if (board[i    ][j + 1] === 1) neighborSum++;
if (board[i + 1][j + 1] === 1) neighborSum++;

Just as with the Wolfram CA, I find myself writing out a bunch of if statements. This is another situation where, for teaching purposes, it’s useful and clear to write the code this way, explicitly stating every step (each time a neighbor has a state of 1, the counter increases). Nevertheless, it’s a bit silly to say, “If the cell state equals 1, add 1 to a counter” when I could instead just say, “Add every cell state to a counter.” After all, if the state can be only 0 or 1, the sum of all the neighbors’ states will yield the total number of live cells. Since the neighbors are arranged in a mini 3$\times$3 grid, I can introduce another nested loop to compute the sum more efficiently:

let neighborSum = 0;

for (let k = -1; k <= 1; k++) {
  for (let l = -1; l <= 1; l++) {

    neighborSum += board[i + k][j + l];

  }

}

Of course, I’ve made a significant mistake. In the Game of Life, the current cell doesn’t count as one of the neighbors. I could include a conditional to skip adding the state when both k and l equal 0, but another option is to subtract the cell state after the loop is completed:

neighborSum -= board[i][j];

Finally, when I know the total number of live neighbors, I can decide what the cell’s new state should be according to the rules—birth, death, or stasis:

if (board[i][j] === 1 && neighborSum < 2) {
  next[i][j] = 0;

} else if (board[x][y] === 1 && neighborSum >  3) {
  next[i][j] = 0;

} else if (board[x][y] === 0 && neighborSum === 3) {
  next[i][j] = 1;

} else {
  next[i][j] = board[i][j];
}

Putting this all together:

let next = create2DArray(columns, rows);

for (let i = 1; i < columns - 1; i++) {
  for (let j = 1; j < rows - 1; j++) {

    let neighborSum = 0;
    for (let k = -1; k <= 1; k++) {
      for (let l = -1; l <= 1; l++) {
        neighborSum += board[i + k][j + l];
      }
    }

    neighborSum -= board[i][j];

    if (board[i][j] === 1 && neighborSum < 2) next[i][j] = 0;
    else if (board[i][j] === 1 && neighborSum > 3) next[i][j] = 0;
    else if (board[i][j] === 0 && neighborSum === 3) next[i][j] = 1;
    else next[i][j] = board[i][j];

  }

}

board = next;

Now I just need to draw the board. I’ll draw a square for each spot: white for off, black for on.

  for (let i = 0; i < columns; i++) {

    for (let j = 0; j < rows; j++) {

      fill(255 - board[i][j] * 255);

      stroke(0);

      square(i * w, j * w, w);

    }

  }

In this example, I’m introducing yet another method for drawing the squares based on a cell’s state. Remember, multiplying the cell’s state by 255 gives a white fill color for on and black for off. To invert this, I start with 255 and subtract the cell’s state multiplied by 255: black for on and white for off.

Object-Oriented Cells

Over the course of this book, I’ve built examples of systems of objects that have properties and move about the canvas. In this chapter, although I’ve been talking about a cell as if it were an object, I haven’t used the principles of object orientation in the code. This has worked because a cell is such
an enormously simple object; its only property is its state, a single 0 or 1. However, I could further develop CA systems in plenty of ways beyond the simple models discussed here, and often these
may involve keeping track of multiple properties for each cell. For example, what if a cell needs to remember its history of states? Or what if you want to apply motion and physics to a CA and have the cells move about the canvas, dynamically changing their neighbors from frame to frame?

To accomplish any of these ideas (and more), it would be helpful to see how to treat each cell as an object, rather than as a single 0 or 1 in an array. In a Game of Life simulation, for example, I’ll no longer want to initialize each cell like this:

     board[i][j] = floor(random(2));    

Instead, I want something like this:

     board[i][j] = new Cell(floor(random(2)));

Here, Cell is a new class that I’ll write. What are the properties of a Cell object? In the Game of Life example, I might choose to create a cell that stores its position and size along with its state:

class Cell {

  constructor(state, x, y, w) {

    this.state = state;

    this.x = x;
    this.y = y;
    this.w = w;

In the non-OOP version, I used separate 2D arrays to keep track of the states for the current and next generations. By making a cell an object, however, each cell could keep track of both states by introducing a variable for the previous state:

    this.previous = this.state;
  }

Suddenly, with these additional properties, the cell’s visualization can incorporate more information about the state. For example, what if each cell were colored based on whether its state has changed from one frame to another?

  show() {

    stroke(0);

    if (this.previous === 0 && this.state === 1) {
      fill(0, 0, 255);

    } else if (this.state === 1) {

      fill(0);

    } else if (this.previous === 1 && this.state === 0) {
      fill(255, 0, 0);

    } else {

      fill(255);

    }

    square(this.x, this.y, this.w);

  }

Not much else about the code has to change (at least for my purposes here). The neighbors can still be counted the same way; the difference is that the neighbors’ previous states are counted, and the cell’s new state property is updated. Encapsulating this logic into a calculateState() method that takes board as an argument might also be beneficial. I’ll leave that as an exercise for you.

The following is the Game of Life logic, adapted for cell objects but excluding the calculateState() enhancement:

  for (let x = 1; x < columns - 1; x++) {

    for (let y = 1; y < rows - 1; y++) {

      let neighborSum = 0;

      for (let i = -1; i <= 1; i++) {

        for (let j = -1; j <= 1; j++) {

          neighborSum += board[x + i][y + j].previous;

        }

      }

      neighborSum -= board[x][y].previous;

      if (board[x][y].state === 1 && neighborSum < 2) {
        board[x][y].state = 0;
      } else if (board[x][y].state === 1 && neighborSum > 3) {
        board[x][y].state = 0;
      } else if (board[x][y].state === 0 && neighborSum === 3) {
        board[x][y].state = 1;
      }

    }

  }

}

By transforming the cells into objects, numerous possibilities emerge for enhancing the cells’ properties and behaviors. For example, what if each cell had a lifespan property that increments with each cycle and influences its color or shape over time? Or imagine if a cell had a terrain property that could be land, water, mountain, or forest. How could a 2D CA integrate into a tile-based strategy game or other context?

Variations on Traditional CA

Now that I’ve covered the basic concepts, algorithms, and programming strategies behind the most famous 1D and 2D CA, it’s time to think about how you might take this foundation of code and build on it, developing creative applications of CAs in your own work. In this section, I’ll talk through some ideas for expanding the features of a CA. Example answers to these exercises can be found on the book’s website.

Nonrectangular Grids

There’s no particular reason to limit yourself to placing your cells in a rectangular grid. What happens if you design a CA with another type of shape?

function drawHexagon(x, y, r) {

  push();

  translate(x, y);

  stroke(0);

  beginShape();

  for (let angle = 0; angle < TWO_PI; angle += PI / 3) {

    let xoff = cos(angle) * r;

    let yoff = sin(angle) * r;

    vertex(xoff, yoff);

  }

  endShape(CLOSE);

  pop();

}

Probabilistic

The rules of a CA don’t necessarily have to define an exact outcome.

Continuous

This chapter has focused on examples with a finite number of discrete cell states—either 0 or 1. What if the cell’s state could be any floating-point number from 0 to 1?

Image Processing

I briefly touched on this earlier, but many image-processing algorithms operate on CA-like rules. For example, blurring an image requires creating a new pixel out of the average of a neighborhood of pixels. Simulations of ink dispersing on paper or water rippling over an image can also be achieved with CA rules.

Moving Cells

In these basic examples, cells have a fixed position on a grid, but you could build a CA with cells that have no fixed position and instead move about the canvas.

Nesting

As discussed in Chapter 5, a feature of complex systems is that they can be nested. A city is a complex system of people, a person is a complex system of organs, an organ is a complex system of cells, and so on. How could this be applied to a CA?

The Ecosystem Project

Incorporate CA into your ecosystem. Here are some possibilities:

• Give each creature a state. How can that state drive its behavior? Taking inspiration from CA, how can that state change over time according to its neighbors’ states?
• Consider the ecosystem’s world to be a CA. The creatures move from tile to tile, and each tile has a state. Is it land? Water? Food?
• Use a CA to generate a pattern for the design of a creature in your ecosystem.