Chapter 8: Fractals
“Pathological monsters!” cried the terrified mathematician
Every one of them a splinter in my eye
I hate the Peano Space and the Koch Curve
I fear the Cantor Ternary Set
The Sierpiński Gasket makes me wanna cry
And a million miles away a butterfly flapped its wings
On a cold November day a man named Benoit Mandelbrot was born
—Jonathan Coulton, lyrics from “Mandelbrot Set”

The Chakri Maha Prasat Hall, located within the Grand Palace in the heart of Bangkok, Thailand, is an architectural feat known for its intricate details and grandeur. Each level of the multilayered roof echoes a smaller or larger version of itself and represents the different levels of Mount Meru, the center of the Buddhist universe.
Once upon a time, I took a course in high school called Geometry. Perhaps you took such a course too, where you learned about classic shapes in one, two, and maybe even three dimensions. What’s the circumference of a circle? The area of a rectangle? The distance between a point and a line? This sort of geometry is generally referred to as Euclidean geometry, after the Greek mathematician Euclid, and come to think of it, it’s a subject I’ve been covering all along in this book. Whenever I used vectors to describe the motion of bodies in Cartesian space, that was Euclidean geometry.
For us nature coders, however, I would ask, Can our world really be described with Euclidean geometry? The laptop screen I’m staring at right now sure looks like a rectangle. And the plum I ate this morning was spherical. But what if I were to look further and consider the trees that line the street, the leaves that hang off those trees, the lightning from last night’s thunderstorm, the cauliflower I ate for dinner, the blood vessels in my body, and the mountains and coastlines that define a landscape? As Figure 8.1 shows, most of the stuff you find in nature looks quite different from the idealized geometrical forms of Euclidean geometry.
If you want to start building computational designs with patterns that move beyond basic shapes like circle(), square(), and line(), it’s time to learn about a different kind of geometry, the geometry of nature: fractals. This chapter explores the concepts behind fractals as well as programming techniques for simulating fractal geometry.
What Is a Fractal?
The term fractal (from the Latin fractus, meaning “broken”) was coined by the mathematician Benoit Mandelbrot in 1975. In his seminal work The Fractal Geometry of Nature, he defines a fractal as “a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole.”
I’ll illustrate this definition with two simple examples. First, think about the branching structure of a tree, as shown in Figure 8.2. (In Example 8.6, I’ll show you how to write the code to draw this tree.)
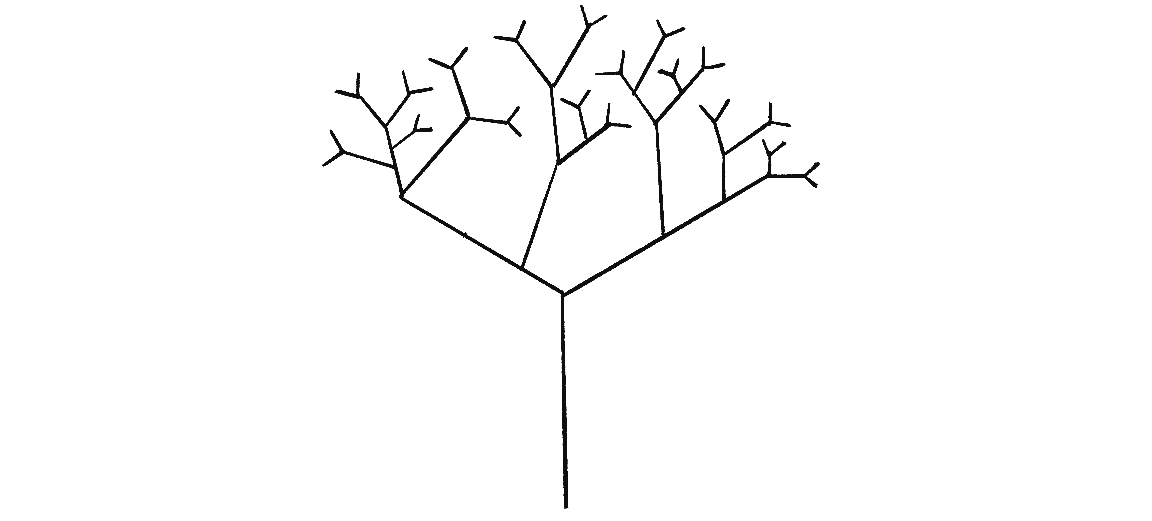
Notice that the tree has a single trunk with branches connected at its end. Each one of those branches has branches at its end, and those branches have branches, and so on. And what if you were to pluck one branch from the tree and examine it more closely on its own, as in Figure 8.3?
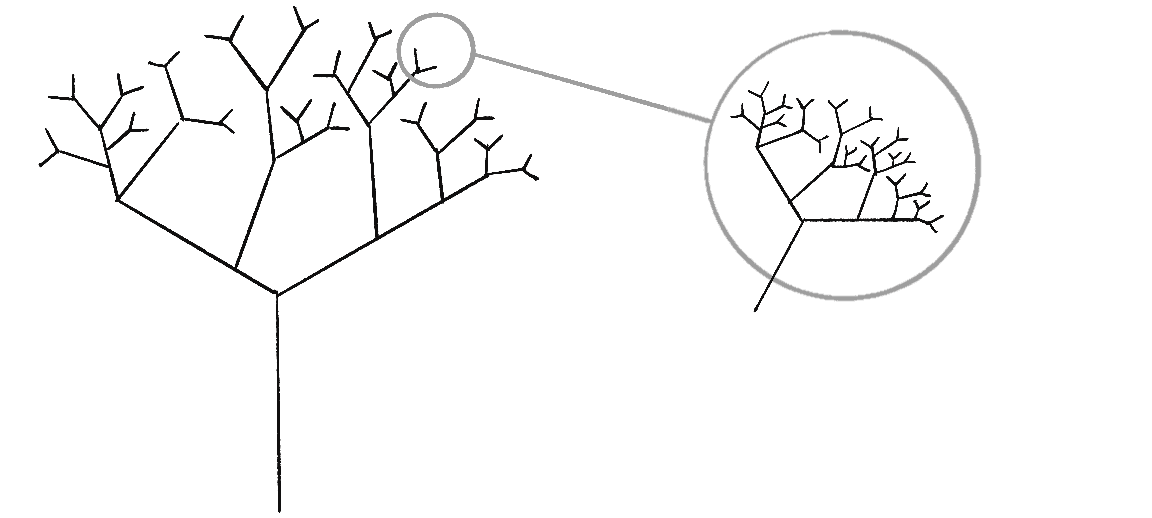
The zoomed-in branch is an exact replica of the whole, just as Mandelbrot describes. Not all fractals have to be perfectly self-similar like this tree, however. For example, take a look at Figure 8.4, which shows two illustrations of the coastline of Greenland (or Kalaallit Nunaat in the indigenous Kalaallisut language).
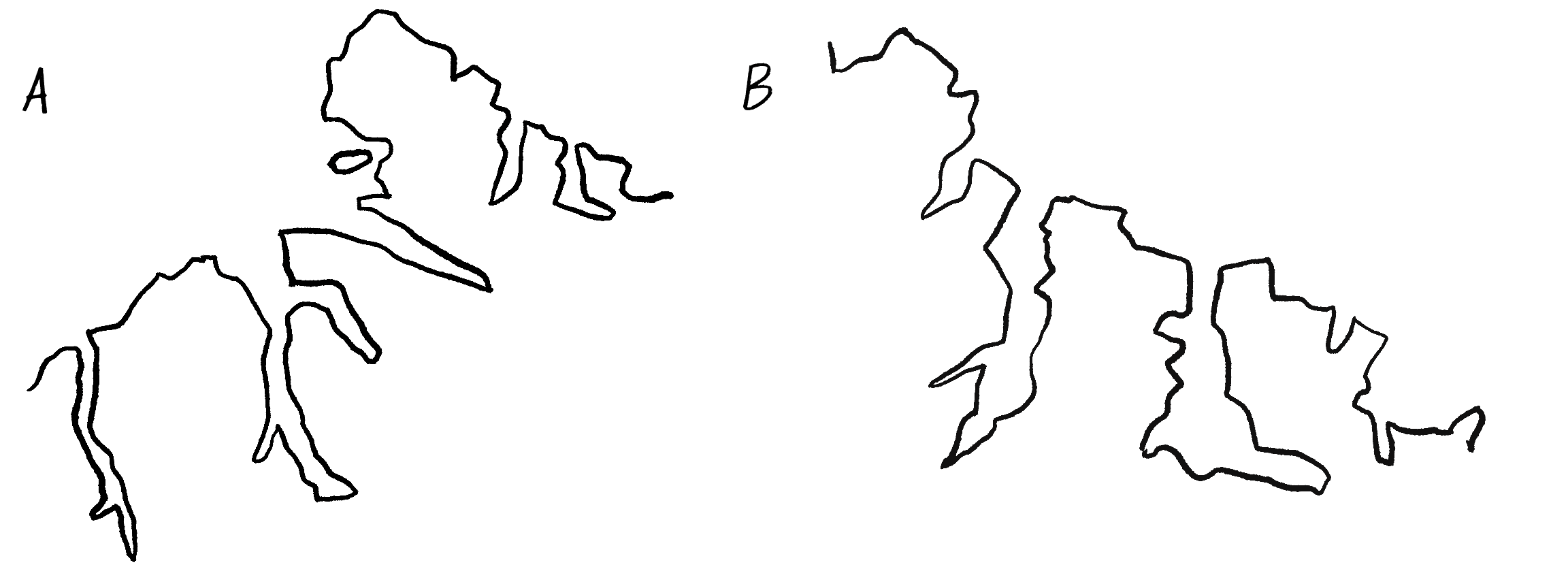
The absence of a scale in these illustrations is no accident. Am I showing the entire coastline or just a small portion of it? There’s no way for you to know without a scale reference because coastlines, as fractals, look essentially the same at any scale. (Incidentally, coastline B shows an approximately 3 magnified view of a specific section of coastline A. I’ve added the scales in Figure 8.5.)
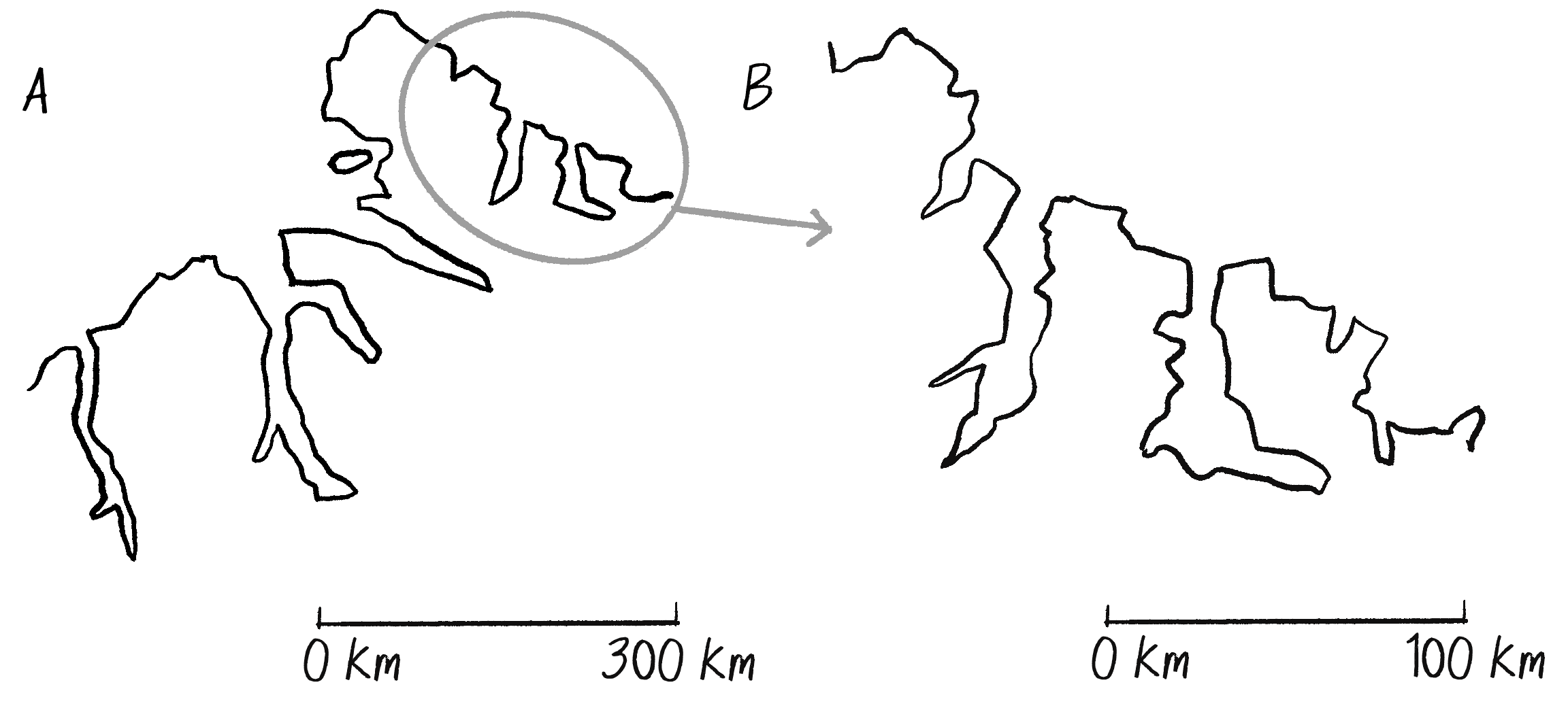
A coastline is an example of a stochastic fractal, meaning it’s built out of probabilities and randomness. Unlike the deterministic (or predictable) tree-branching structure, a stochastic fractal is statistically self-similar. This means that even if a pattern isn’t precisely the same at every size, the general quality of the shape and its overall feel stay the same no matter how much you zoom in or out. The examples in this chapter explore both deterministic and stochastic techniques for generating fractal patterns.
While self-similarity is a key trait of fractals, it’s important to realize that self-similarity alone doesn’t make a fractal. After all, a straight line is self-similar: it looks the same at any scale and can be thought of as comprising lots of little lines. But a straight line isn’t a fractal. Fractals are characterized by having a fine structure at small scales (keep zooming in on the coastline and you’ll continue to find fluctuations) and can’t be described with Euclidean geometry. As a rule, if you can say “It’s a line!” then it’s not a fractal.
The Mandelbrot Set
One of the most well-known and recognizable fractal patterns is named for Mandelbrot himself. Generating the Mandelbrot set involves testing the properties of complex numbers after they’re passed through an iterative function. Do they tend to infinity? Do they stay bounded?
While a fascinating mathematical discussion, this escape-time algorithm is a less practical method for generating fractals than the recursive techniques we’ll examine in this chapter. For more on how to visualize the Mandelbrot set with p5.js, you can check out the related Coding Challenge page on the Coding Train website.

Fractals have a long history predating Mandelbrot’s 1975 book, appearing in various forms across cultures. They’re virtually as old as nature itself. Indigenous and ancient societies often incorporated fractal patterns into their art, architecture, and textiles, long before the formal study of fractals in Western mathematics. For example, the traditional Ba-ila village layouts of Zambia and the intricate geometric patterns in Islamic architecture both exhibit fractal properties. These patterns highlight the significance of fractals in diverse cultural contexts and their timeless appeal.
Recursion
Beyond self-similarity, another fundamental component of fractal geometry is recursion: the process of repeatedly applying a rule, known as a production rule, indicating that the outcome of one iteration becomes the starting point for the next. Recursion has been in the picture since the first appearance of fractals in modern mathematics, when German mathematician Georg Cantor developed simple rules for generating an infinite set of numbers in 1883. Cantor’s production rules are illustrated in Figure 8.6.

A feedback loop is at work in Cantor’s rules. Take a single line and break it into two. Then return to those two lines and apply the same rule, breaking each line into two. Now you have four. Return to those four lines and apply the rule. Now you have eight. And so on. That’s how recursion works: the output of a process is fed back into the process itself, over and over again. In this case, the result is known as the Cantor set. Like the fractal tree in Figure 8.3, it’s an example of a deterministic, entirely predictable fractal, in which each part is a precise replica of the whole.
Cantor was interested in what happens when you apply a recursive set of rules an infinite number of times. You and I don’t have infinite time on our hands, however. Also, a p5.js sketch is limited to a finite pixel space, so at some point it becomes impossible to draw increasingly smaller lines. As such, for the purposes of this book, I’ll mostly ignore the questions and paradoxes that arise from infinite recursion. Instead, the code will be constructed in such a way that the rules aren’t applied “forever” (resulting in an infinite loop and a frozen computer) but instead stop when a certain condition is met.
Implementing Recursive Functions
In a moment, I’ll write a sketch that recursively implements the Cantor set. But first, what does it mean to have recursion in code? It all boils down to calling a function from inside a function. This, in and of itself, isn’t anything new. After all, you probably call functions from inside other functions all the time. For example:
function someFunction() {
background(0);
Call the function background() in the definition of someFunction().
}
Here’s the key difference with recursion: What would happen if you called the function you’re defining within that function itself? Can someFunction() call someFunction()?
function someFunction() {
someFunction();
Is this a paradox?
}
Not only is this allowed, but it’s quite encouraged! In fact, it’s essential to the way I’ll implement the Cantor set. Functions that call themselves are known as recursive functions, and they’re well suited for solving certain problems. For example, some mathematical calculations are implemented recursively; the most well-known example is the factorial.
The factorial of any number n, usually written as n!, is defined as follows:
Here’s a nonrecursive function in JavaScript that uses a for loop to calculate the factorial of a number:
function factorial(n) {
let value = 1;
for (let i = 0; i < n; i++) {
value = value * (i + 1);
}
Use a regular loop to compute the factorial.
return value;
}
Upon close examination, you’ll notice something interesting about the way factorials work. Think about how 4! and 3! are defined:
The entire definition of 3! is contained within the definition of 4!:
In more general terms, for any positive integer n, the following is true:
Writing this out, I can say that the factorial of n is defined as n times the factorial of n – 1.
The definition of factorial includes factorial? That’s kind of like defining pizza as “a delicious meal that includes slices of pizza.” While this definition of pizza is admittedly nonsensical, it highlights the concept of self-reference in a definition, the essence of recursion. When applied to a function definition in code, it can lead to remarkably elegant solutions, such as this recursive definition of a factorial() function:
function factorial(n) {
if (n <= 1) {
return 1;
} else {
return n * factorial(n - 1);
}
}
The factorial() function calls itself within its own definition. It may look a bit odd at first, but it works, as long as a stopping condition exists (in this case, n <= 1) so the function doesn’t get stuck calling itself forever. (I’m using <= instead of === as a safeguard against infinite recursion, but I should probably include additional error checking to manage noninteger or negative inputs to be more mathematically accurate.) Figure 8.7 illustrates the steps that unfold when factorial(4) is called.
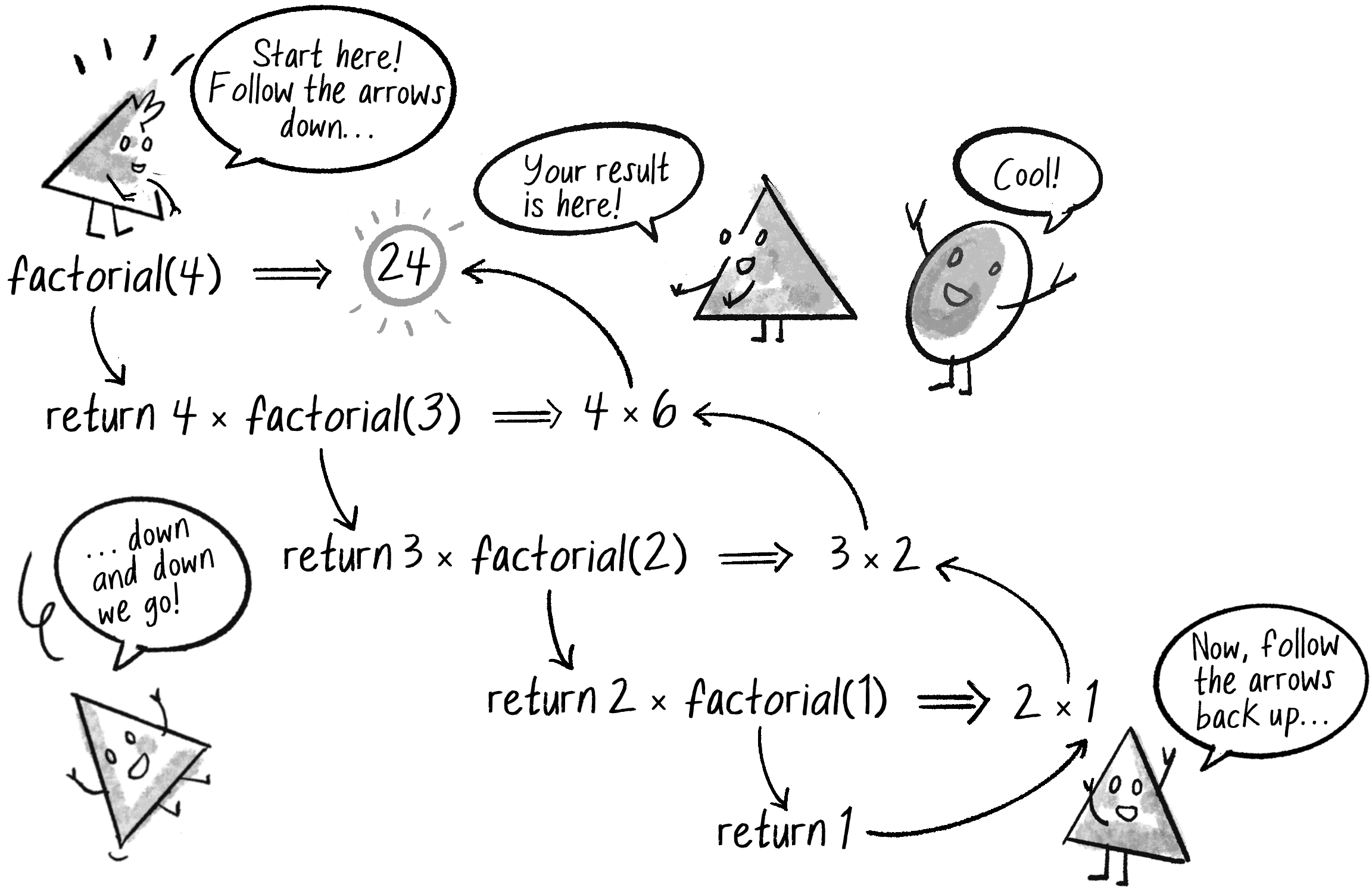
factorial() functionThe function keeps calling itself, descending deeper and deeper down a rabbit hole of nested function calls until it reaches the stopping condition. Then it works its way up out of the hole, returning values until it arrives back home at the original call of factorial(4).
You can apply the same recursive principle illustrated by the factorial() function to graphics in a canvas, only instead of returning values, you draw shapes. This is precisely what you’ll see in the examples throughout this chapter. To begin, here’s a simple recursive function that draws increasingly smaller circles.
Example 8.1: Recursive Circles Once
function drawCircles(x, y, r) {
circle(x, y, r * 2);
if (r > 4) {
Exit condition: stop when the radius is too small.
r *= 0.75;
drawCircles(x, y, r);
Call the function inside the function (aka recursion!).
}
}
The drawCircles() function draws a circle based on a set of parameters that it receives as arguments. It then calls itself with those same parameters, adjusting them slightly. The result is a series of circles, each of which is drawn inside the previous circle.
Just as the factorial() function stops recursing when n equals 0, notice that drawCircles() recursively calls itself only if the radius is greater than 4. This is a crucial point. As with iteration, all recursive functions must have an exit condition! You’re likely already aware that all for and while loops must include a Boolean expression that eventually evaluates to false, thus exiting the loop. Without one, the sketch would get caught inside an infinite loop. The same can be said about recursion. If a recursive function calls itself forever and ever with no exit, you’d be treated to a chilly, frozen screen in most cases. The browser, however, has protections built in, and rather than freeze, it will quit the sketch with the error message Maximum call stack size exceeded. This is just a fancy way of saying, “Too many recursive calls to the same function; time to stop!”
Example 8.1 was rather trivial; it could easily be achieved through simple iteration with a for or while loop. The results become more interesting, however, when a function is defined to call itself more than once. In such scenarios, recursion becomes wonderfully elegant. To illustrate, I’ll make drawCircles() a bit more complex: for every circle displayed, draw two more circles inside it, half its size—one left of center and one right of center.
Example 8.2: Recursive Circles Twice
function setup() {
createCanvas(640, 240);
}
function draw() {
background(255);
drawCircles(width / 2, height / 2, 320);
}
function drawCircles(x, y, radius) {
stroke(0);
noFill();
circle(x, y, radius * 2);
if (radius > 4) {
drawCircles(x + radius / 2, y, radius / 2);
drawCircles(x - radius / 2, y, radius / 2);
drawCircles() calls itself twice. For every circle, a smaller circle is drawn to the left and the right.
}
}
Add two more lines of code, and now each circle contains four circles—left, right, above, and below its center.
Example 8.3: Recursive Circles Four Times
function drawCircles(x, y, radius) {
stroke(0);
noFill();
circle(x, y, radius * 2);
if (radius > 16) {
drawCircles(x + radius / 2, y, radius / 2);
drawCircles(x - radius / 2, y, radius / 2);
drawCircles(x, y + radius / 2, radius / 2);
drawCircles(x, y - radius / 2, radius / 2);
drawCircles() calls itself four times.
}
}
Try reproducing this sketch with iteration instead of recursion—I dare you!
Drawing the Cantor Set with Recursion
Now that I’ve demonstrated how to use recursive functions, I’m ready to visualize the Cantor set in p5.js. Where do I begin? Well, I know that the Cantor set begins with a line, so I’ll start there and write a function that draws a line:
function cantor(x, y, length) {
line(x, y, x + length, y);
}
This function draws a line of length length that starts at pixel coordinate (x, y). The line is drawn horizontally, but this is an arbitrary decision. Let’s say the function is called like so:
cantor(10, 20, width - 20);
You’d see something like Figure 8.8.

cantor() is a single line.
The Cantor rule operates by duplicating the original line and erasing its middle third section, leaving two remaining lines—one from the beginning to the one-third mark, and one from the two-thirds mark to the end of the line (see Figure 8.9). I can implement that rule manually by calling line() two more times, moving the y-position down 20 pixels so that the next generation of lines appears below the first.
function cantor(x, y, length) {
line(x, y, x + length, y);
line(x, y + 20, x + length / 3, y + 20);
From start to one-third
line(x + (2 * length) / 3, y + 20, x + length, y + 20);
From two-thirds to the end
}
Figure 8.10 shows the result.

This works over two generations, but continuing to manually call line() will quickly become unwieldy. For the succeeding generations, I’d need 4, then 8, then 16 calls to line(). A for loop is the usual way around such a problem, but give that a try and you’ll see that working out the math for each iteration quickly proves inordinately complicated. Don’t despair, however: here’s where recursion comes to the rescue!
Look at where I draw the first line of the second generation, from the start to the one-third mark:
line(x, y + 20, x + length / 3, y + 20);
Instead of calling the line() function directly, why not call the cantor() function? After all, what does the cantor() function do? It draws a line at an (x, y) position with a given length. The x value stays the same, y increments by 20, and the length is length / 3:
cantor(x, y + 20, length / 3);
This call to cantor() is precisely equivalent to the earlier call to line(). And for the next line in the second generation, I can call cantor() again:
cantor(x + (2 * length / 3), y + 20, length / 3);
Now the cantor() function looks like this:
function cantor(x, y, length) {
line(x, y, x + len, y);
cantor(x, y + 20, length / 3);
cantor(x + (2 * length / 3), y + 20, length / 3);
Two recursive calls. Note that 20 pixels are added to y.
}
Since the cantor() function is now recursive, the same rule will be applied to the next line and to the next and to the next as cantor() calls itself again and again! But don’t go running this code quite yet. The sketch is missing that crucial element: an exit condition. It has to stop recursing at some point. Here, I’ll choose to stop if the line length is less than or equal to 1 pixel. In other words, keep going if length is greater than 1.
Example 8.4: The Cantor Set
function cantor(x, y, length) {
if (length > 1) {
Keep going as long as the length is greater than 1.
line(x, y, x + length, y);
cantor(x, y + 20, length / 3);
cantor(x + (2 * length) / 3, y + 20, length / 3);
}
}
Writing a function that recursively calls itself is a simple, elegant technique for generating a fractal pattern, but it doesn’t allow me to do much beyond drawing the pattern. For example, what if I want the lines in the Cantor set to exist as individual objects that could be moved independently? For that, I need to use a different programming approach, one that applies recursion in combination with an array that keeps track of all its individual parts. That’s exactly what I’ll do next!
Exercise 8.1
Using Examples 8.2 and 8.3 as a model, design your own recursive pattern. Here is an example of one using lines.
The Koch Curve
I’ll now turn to another famous fractal pattern, the Koch curve, discovered in 1904 by Swedish mathematician Helge von Koch. Figure 8.11 outlines the production rules for drawing this fractal. Notice that the rules start the same way as the Cantor set, with a single line that’s then divided into three equal parts.
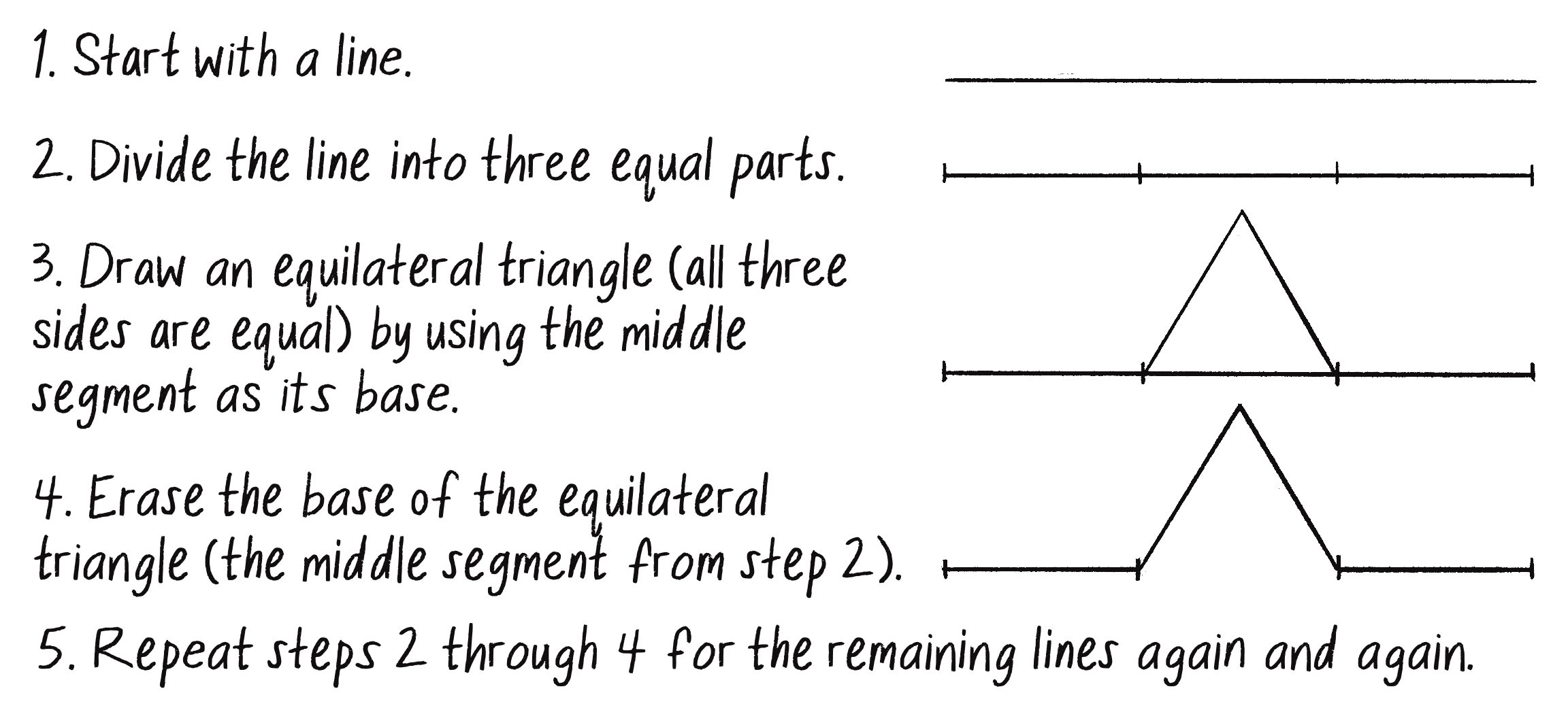
Figure 8.12 shows how the fractal develops over several repetitions of these steps.

I could proceed in the same manner as I did with the Cantor set and write a recursive function that iteratively applies the Koch rules over and over. Instead, I’m going to tackle this problem differently by treating each segment of the Koch curve as an individual object. This will open up some exciting design possibilities. For example, if each segment is an object, it could move independently from its original position and participate in a physics simulation. In addition, the visual appearance of each segment could vary if the object includes customizable properties for color, line thickness, and so on.
The Monster Curve
The Koch curve and other fractal patterns are often called mathematical monsters because of an odd paradox that emerges when you apply the recursive definition an infinite number of times. If the length of the original starting line is 1, the first iteration of the Koch curve will yield a line of length four-thirds (each segment is one-third the length of the starting line). Do it again and you get a length of sixteen-ninths. As you iterate toward infinity, the length of the Koch curve approaches infinity, and yet it fits in the tiny finite space provided right here on this paper (or screen)!
Since you’re working in the p5.js land of finite pixels, this theoretical paradox won’t be a factor. You’ll just have to limit the number of times you recursively apply the Koch rules so that your program won’t run out of memory or crash.
To accomplish the goal of treating each segment as an individual object, I must first decide what this object should be in the first place. What data should it store? What functions should it have? The Koch curve is a series of connected lines, and so I’ll think of each segment as a KochLine. Each KochLine object has a start point (a) and an end point (b). These points are represented as p5.Vector objects, and the line is drawn using the line() function:
class KochLine {
constructor(a, b) {
A line between two points: a and b
this.start = a.copy();
this.end = b.copy();
a and b are p5.Vector objects.
}
show() {
stroke(0);
line(this.start.x, this.start.y, this.end.x, this.end.y);
Draw the line from a to b.
}
}
Now that I have the KochLine class, I can get started on setup() and draw(). I’ll need a data structure to keep track of what will eventually become many KochLine objects, and a JavaScript array will do just fine (see Chapter 4 for a review of arrays):
let segments = [];
In setup(), I’ll want to add the first line segment to the array, a line that stretches from 0 to the width of the canvas:
function setup() {
createCanvas(640, 240);
let start = createVector(0, 200);
Left side of the canvas
let end = createVector(width, 200);
Right side of the canvas
segments.push(new KochLine(start, end));
The first KochLine object
}
Then in draw(), all KochLine objects (just one for now) can be rendered with a for...of loop:
function draw() {
background(255);
for (let segment of segments) {
segment.show();
}
}
This is my foundation for the sketch. I have a KochLine class that keeps track of a line from point start to point end, and I have an array that keeps track of all the KochLine objects. Given these elements, how and where should I apply the Koch rules and the principles of recursion?
Remember the Game of Life cellular automaton from Chapter 7? In that simulation, I always kept track of two generations: current and next. When I was finished calculating the next generation, next became current, and I moved on to computing the new next generation. I’m going to apply a similar technique here. I have a segments array listing the current set of line segments (at the start of the program, there’s only one). Now I need a second array (I’ll call it next), where I can place all the new KochLine objects generated from applying the Koch rules. For every single KochLine in the current array, four new line segments will be added to next. When I’m done, the next array becomes the new segments array (see Figure 8.13).
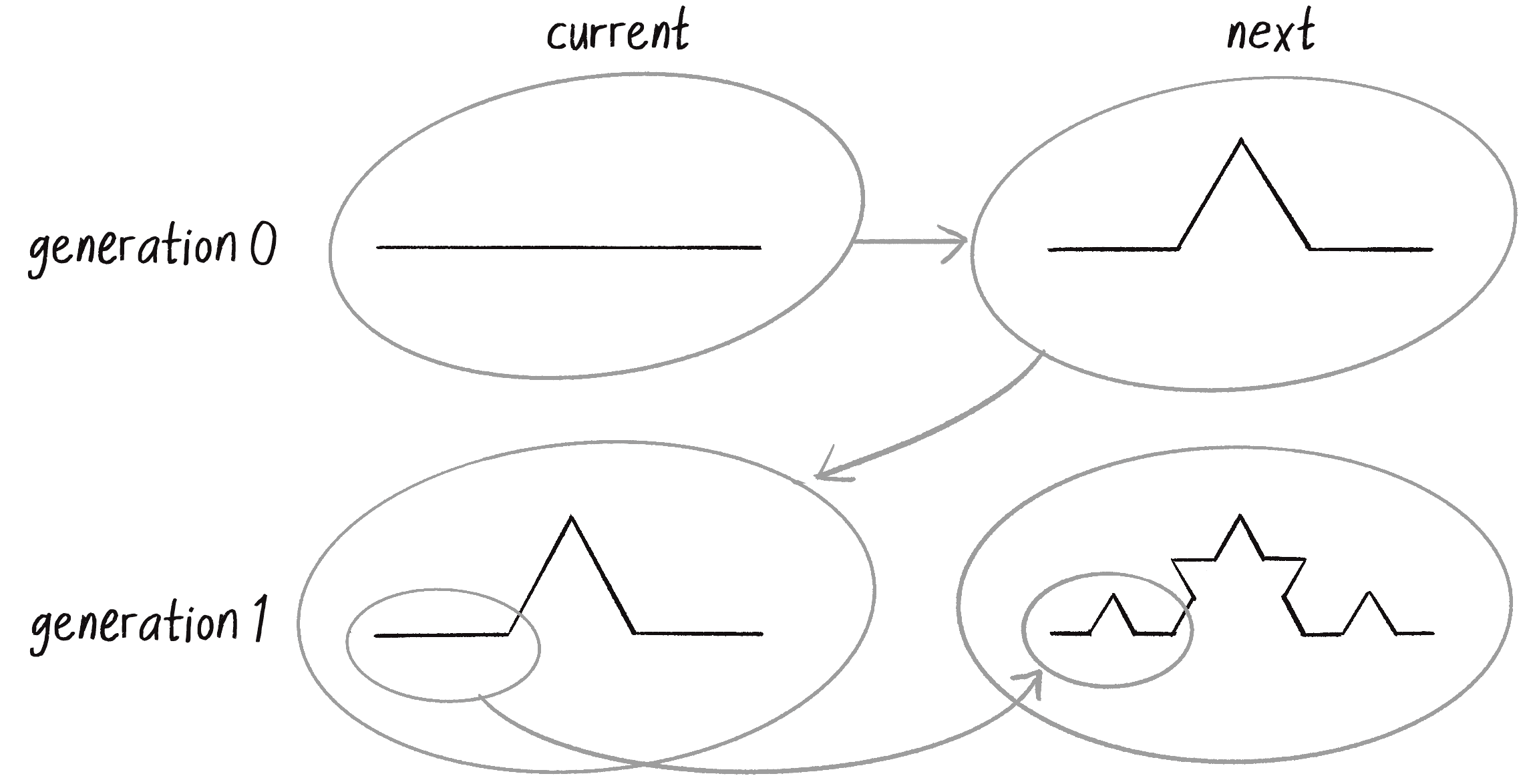
Here’s how the code looks:
function generate() {
let next = [];
Create the next array.
for (let segment of segments) {
For every segment . . .
next.push(new KochLine(????, ????));
next.push(new KochLine(????, ????));
next.push(new KochLine(????, ????));
next.push(new KochLine(????, ????));
. . . add four new lines. How do you calculate the start and end points of each?
}
segments = next;
The next segments!
}
By calling generate() over and over, the Koch curve rules will be recursively applied to the existing set of KochLine segments. But, of course, I’ve skipped over the real work of the function: How do I actually break one line segment into four as described by the rules? I need a way to calculate the start and end points of each line.
Because the KochLine class uses p5.Vector objects to store the start and end points, this is a wonderful opportunity to practice all that vector math from Chapter 1, along with some trigonometry from Chapter 3. First, I should establish the scope of the problem: How many points do I need to compute for each KochLine object? Figure 8.14 shows the answer.

As the figure illustrates, I need to turn the two points (start, end) into five (a, b, c, d, e) to generate the four new line segments (a → b, b → c, c → d, d → e):
next.add(new KochLine(a, b));
next.add(new KochLine(b, c));
next.add(new KochLine(c, d));
next.add(new KochLine(d, e));
Where do I get these points? Why not ask the KochLine object to calculate them for me?
function generate() {
let next = [];
for (let segment of segments) {
let [a, b, c, d, e] = segment.kochPoints();
next.push(new KochLine(a, b));
next.push(new KochLine(b, c));
next.push(new KochLine(c, d));
next.push(new KochLine(d, e));
A KochLine needs a method that returns all five points computed according to the Koch rules.
}
segments = next;
}
Wait, let’s take a look at this one line of code a little bit more closely:
let [a, b, c, d, e] = segment.kochPoints();
This is object destructuring, but for an array!
As you may recall, in Chapter 6 I explained object destructuring as a means of extracting properties from an object and assigning them to individual variables. Guess what? You can do the same with arrays! Here, as long as the kochPoints() method returns an array of five elements, I can conveniently unpack and assign them, each to its respective variables: a, b, c, d, and e. It’s a lovely way to handle multiple return values. Just as with objects, array destructuring keeps the code neat and tidy.
Now I just need to write a new kochPoints() method in the KochLine class that returns an array of p5.Vector objects representing the points a through e in Figure 8.15. I’ll knock off a and e first, which are the easiest—they’re just copies of the start and end points of the original line:
kochPoints() {
let a = this.start.copy();
Note the use of copy(). As discussed in Chapter 5, it’s best to avoid making copies whenever
possible, but here a new object is needed in case the segments need to move
independently of each other.
let e = this.end.copy();
How about points b and d? Point b is one-third of the way along the line segment, and d is two-thirds of the way along. As Figure 8.15 shows, if I create a vector that points from the original start to end, I can find the new points by scaling its magnitude to one-third for the new b and two-thirds for the new d.
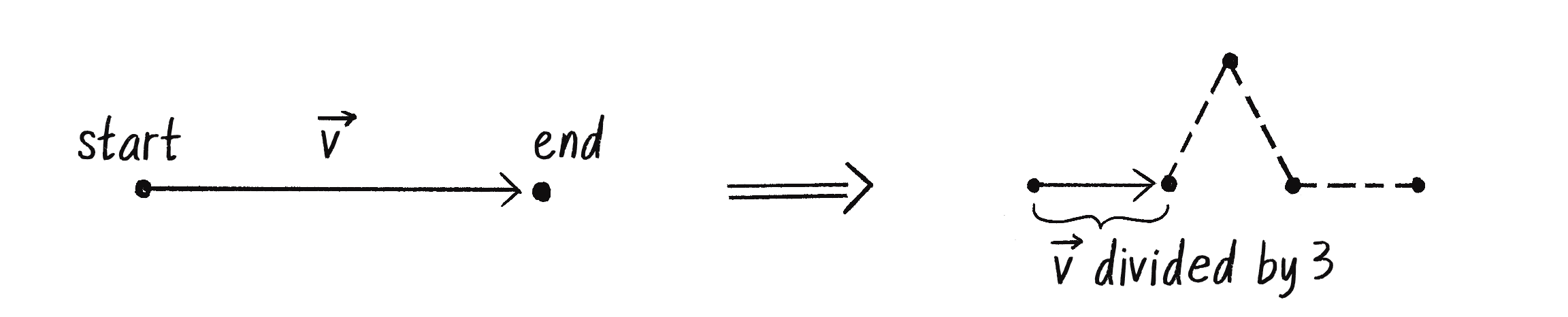
Here’s how that looks in code:
let v = p5.Vector.sub(this.end, this.start);
Create a vector from start to end.
v.div(3);
Shorten the length to one-third.
let b = p5.Vector.add(a, v);
Add that vector to the beginning of the line to find the new point.
let d = p5.Vector.add(b, v);
d is just another one-third of the way past b!
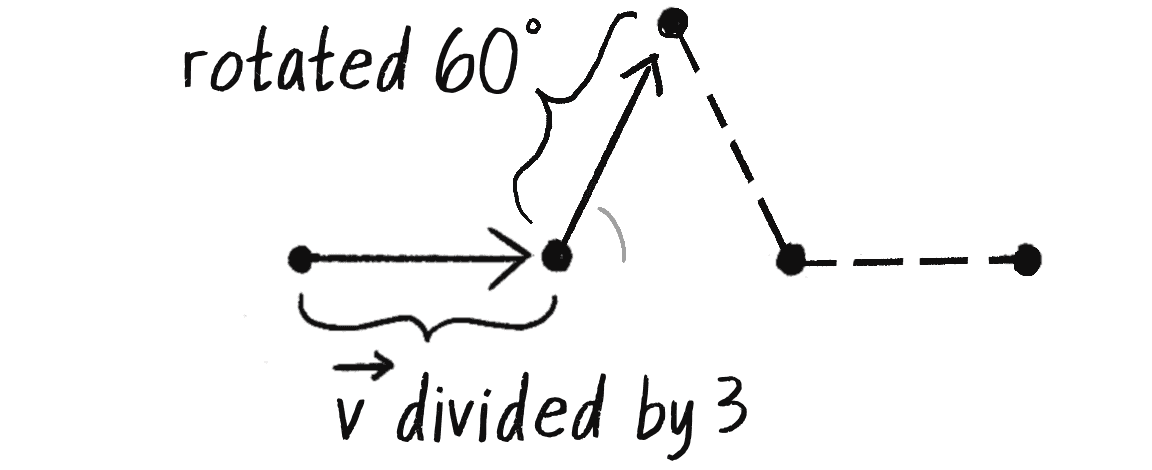
The last point, c, is the most difficult one to compute. However, if you consider that the angles of an equilateral triangle are all 60 degrees, this makes your work suddenly easier. If you know how to find the new b with a vector one-third the length of the line, what if you rotate that same vector 60 degrees (or radians) and add it to b, as in Figure 8.16? You’d arrive at c!
v.rotate(-PI / 3);
Rotate by –π/3 radians (negative angle so it rotates “up”).
let c = p5.Vector.add(b, v);
Move along from b by v to get to point c.
Finally, after calculating the five points, I can return them all together in an array. This will match the code for destructuring the array into five separate variables, as previously outlined:
return [a, b, c, d, e];
}
Return all five points in an array.
Now all that remains is to call generate() a certain number of times (say, five) in setup() to calculate the Koch line segments up to that generation.
Example 8.5: The Koch Curve
let segments = [];
function setup() {
createCanvas(640, 240);
let start = createVector(0, 200);
let end = createVector(width, 200);
segments.push(new KochLine(start, end));
for (let i = 0; i < 5; i++) {
generate();
}
Apply the Koch rules five times.
}
In this example, I chose to call generate() five times. Each time the Koch rules are applied, the number of line segments grows exponentially. It’s an arbitrary decision, but after five iterations I have 1,024 segments, which provide a considerable amount of detail for seeing the pattern. You could, however, choose to use the approach taken in previous examples, setting a threshold for the minimum segment length and calling generate() until the segments become too small. Alternatively, you might consider an interactive option, with a button that advances the shape to the next generation with each press.
Exercise 8.2
Draw the Koch snowflake, which consists of three Koch curves arranged in a triangle. Or draw some another variation of the Koch curve.
Exercise 8.3
Try animating the Koch curve. For example, can you draw it from left to right? Can you vary the visual design of the line segments? Can you move the line segments by using techniques from earlier chapters? What if you make each line segment into a spring (Toxiclibs.js) or constraint (Matter.js)?
Exercise 8.4
Rewrite the Cantor set example by using objects and an array.
Exercise 8.5
Use recursion to draw the Sierpiński triangle (as seen in Chapter 7’s Wolfram elementary CA).

Trees
The fractals presented so far in this chapter have been deterministic: they have no randomness baked in and will always produce the same outcome each time they’re run. While this has made for an excellent introduction to classic fractal patterns and the programming techniques behind drawing them, the results have appeared too precise to seem truly organic.
In this section, I’ll take a step closer to the natural world, with a case study of a branching fractal tree. I’ll start with a deterministic version. Then I’ll introduce an element of randomness to illustrate techniques for generating stochastic (or nondeterministic) fractals, whose outcome can vary each time.
The Deterministic Version
Figure 8.17 outlines a deterministic set of production rules for drawing a fractal tree.
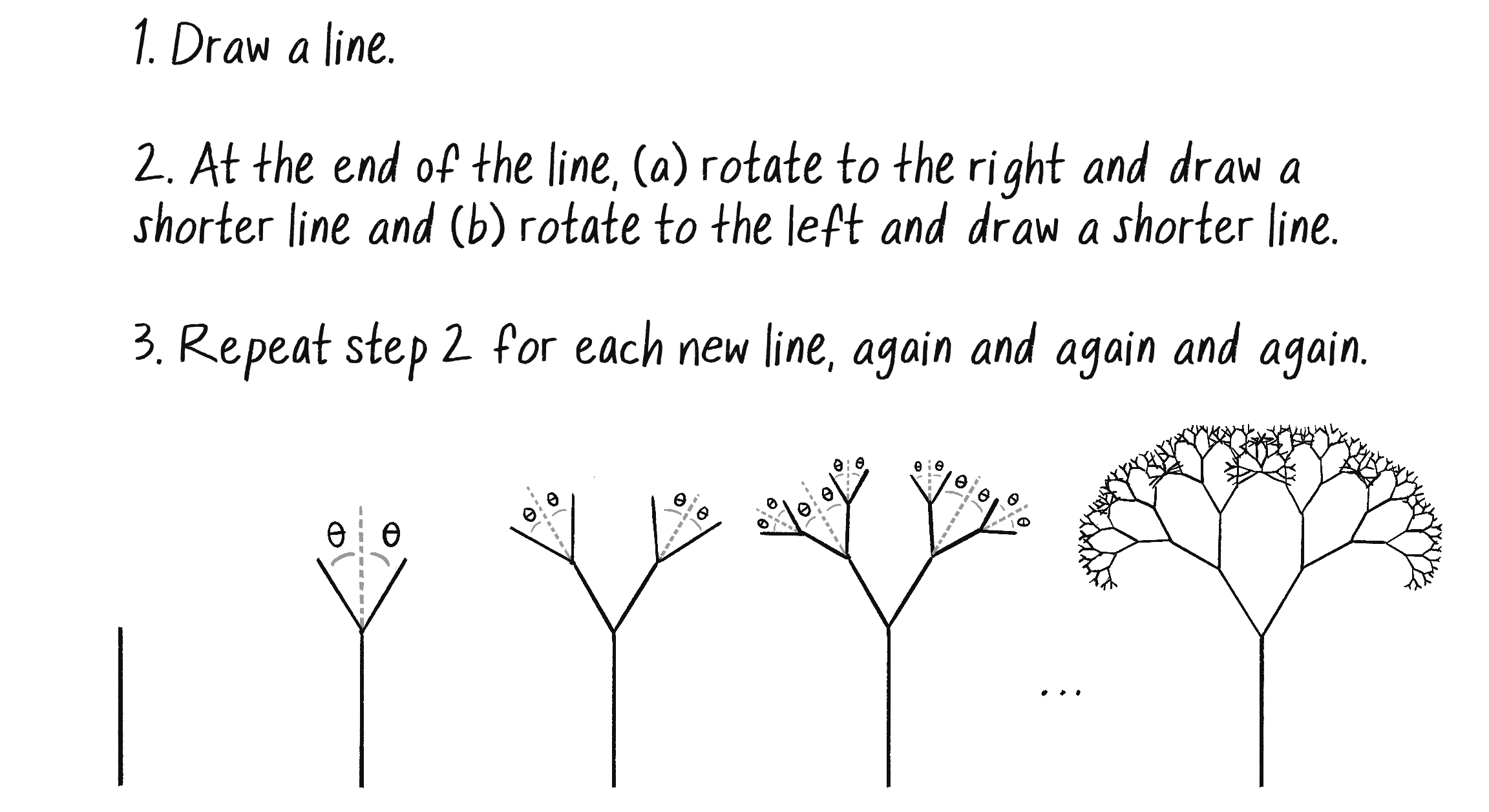
Once again, I have a nice fractal with a recursive definition: a branch is a line with two branches connected to it. What makes this fractal a bit more difficult than the previous ones is the use of the word rotate in the fractal’s rules. Each new branch must rotate relative to the previous branch, which is rotated relative to all its previous branches. Luckily, p5.js has a mechanism to keep track of rotations: transformations.
I touched on transformations in Chapter 3. They’re a set of functions, such as translate(), rotate(), scale(), push(), and pop(), that allow you to change the position, orientation, and scale of shapes in your sketch. The translate() function moves the coordinate system, rotate() rotates it, and push() and pop() help save and restore the current transformation state. If you aren’t familiar with these functions, I have a set of videos on transformations in p5.js available at the Coding Train website.
I’ll begin by drawing a single branch, the trunk of the tree. Since I’m going to be using the rotate() function, I need to make sure I’m continuously translating along the branches while drawing. Remember, when you rotate in p5.js, you’re always rotating around the origin, or point (0, 0), so here the origin must always be translated to the start of the next branch being drawn (equivalent to the end of the previous branch). Since the trunk starts at the bottom of the window, I first have to translate to that spot:
translate(width / 2, height);
Then I can draw the trunk as a line upward:
line(0, 0, 0, -100);
Once I’ve drawn the line, I must translate to the end of that line and rotate in order to draw the next branch, as demonstrated in Figure 8.18. (Eventually, I’m going to need to package up what I’m doing right now into a recursive function, but I’ll sort out the individual steps first.)
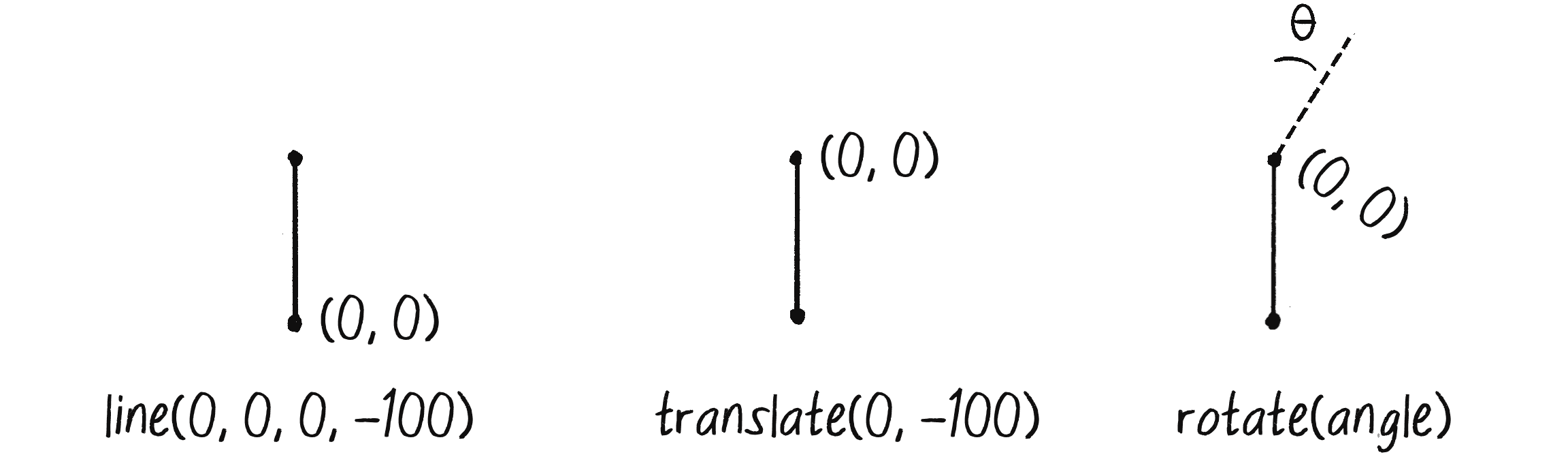
Here’s the code for the process illustrated in Figure 8.18. I’m using an angle of 30 degrees, or radians:
translate(0, -100);
rotate(PI / 6);
line(0, 0, 0, -100);
π divided by 6 is equivalent to 30°.
Now that I have a branch going to the right, I need one going to the left (see Figure 8.19). For that, I should have used push() to save the transformation state before rotating and drawing the right branch. Then I’ll be able to call pop() after drawing the right branch to restore that state, putting me back in the correct position to rotate and draw the left branch.
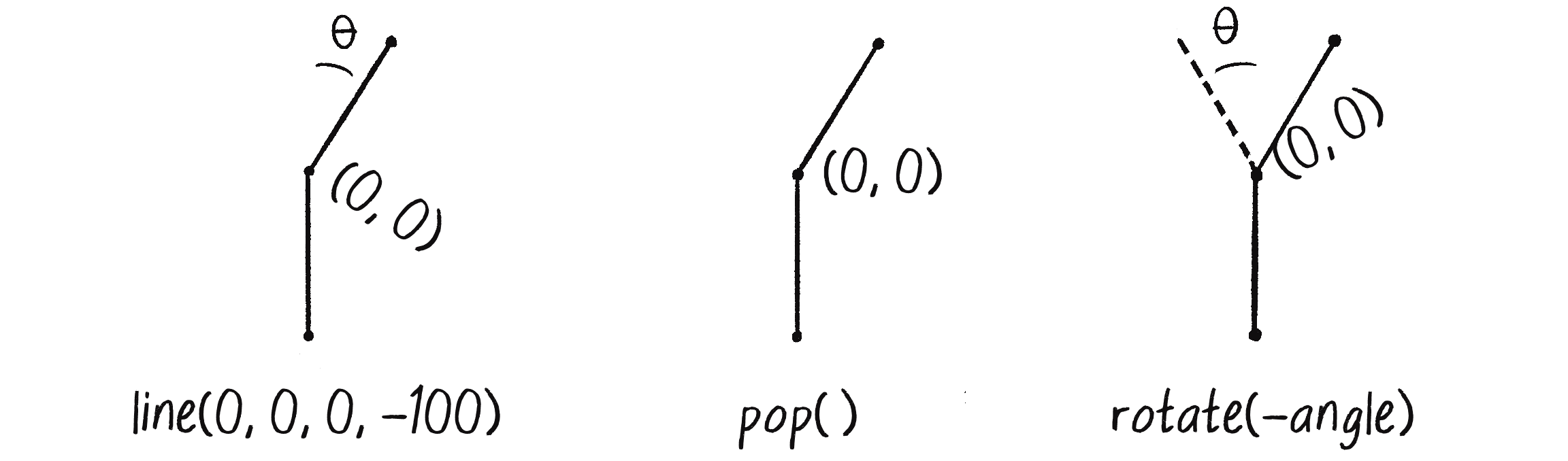
Here’s all the code together:
translate(width / 2, height);
line(0, 0, 0, -100);
The root
translate(0, -100);
push();
rotate(PI / 6);
line(0, 0, 0, -100);
pop();
Branch to the right
rotate(-PI / 6);
line(0, 0, 0, -100);
Branch to the left
Think of each call to the line() function as a branch, and you can begin to see how this code has implemented a definition of branching as a line that has two lines connected to its end. I could keep adding more and more calls to line() for more and more branches, but just as with the Cantor set and Koch curve, my code would soon become incredibly complicated and unwieldy. Instead, I’ll use the code I’ve already written as a foundation for a branch() function, replacing the second and third calls to line() with recursive calls to branch() itself:
function branch() {
line(0, 0, 0, -100);
Draw the branch.
translate(0, -100);
Translate to the end.
push();
rotate(PI / 6);
branch();
Rotate to the right and branch again.
pop();
push();
rotate(-PI / 6);
branch();
Rotate to the left and branch again.
pop();
}
Notice that I use push() and pop() around each pair of calls to rotate() and branch(). This is one of those elegant code solutions that feels like magic. Before each subsequent call to branch(), the code takes a moment to remember that branch’s starting position, so it can come back to it later. If you turn yourself into p5.js for a moment and try to follow the recursive function with pencil and paper, you’ll notice that you end up drawing all the branches to the right first. At the very end of the right side, pop() will send you back along all the branches that were drawn so that you can populate the branches to the left.
Exercise 8.6
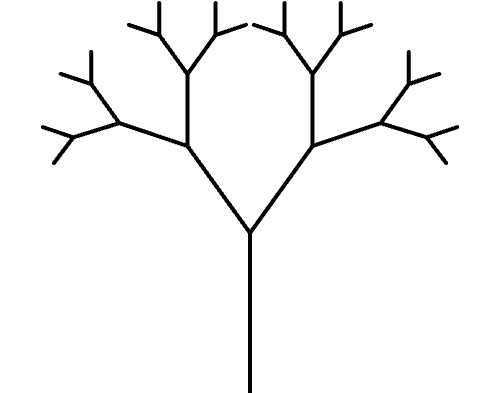
Follow the recursive algorithm of drawing branches, and number them in the diagram in the order that p5.js would actually draw each one.
You may have noticed that the recursive function as written has a major problem: it has no exit condition, so it would get stuck in infinite recursive calls to itself. Also, the branches of the tree should get shorter at each level, but so far I’ve hardcoded every branch to have a length of 100 pixels. The solutions to these two issues are intertwined—if the branches shrink from one generation to the next, I can make the function stop recursing when the branches have become too short:
function branch(len) {
Each branch now receives its length as an argument.
line(0, 0, 0, -len);
translate(0, -len);
len *= 0.67;
Each branch’s length shrinks by one-third.
if (len > 2) {
Exit condition for the recursion!
push();
rotate(angle);
branch(len);
Subsequent calls to branch() include the length argument.
pop();
push();
rotate(-angle);
branch(len);
pop();
}
}
I’ve also included a variable for angle. In the finished example, the angle is controlled by the mouseX position.
Example 8.6: A Recursive Tree
let angle;
function setup() {
createCanvas(640, 240);
}
function draw() {
background(255);
angle = map(mouseX, 0, width, 0, HALF_PI);
Map the angle to range from 0° to 90° (HALF_PI) according to mouseX.
translate(width / 2, height);
stroke(0);
strokeWeight(2);
branch(80);
Start the tree from the bottom of the canvas.
}
The recursive branch() function provides a clean and elegant way of drawing the tree with very few lines of code. However, this approach constrains the potential for animation. By adopting the methodology used in the Koch curve, storing each segment as an object in an array, you can explore creative ways to animate the tree’s growth or even apply physics to the branches!
Exercise 8.7
Vary the strokeWeight() for each branch. Make the trunk thick and each subsequent branch thinner.
Exercise 8.8
Re-create the tree by using a Branch class and an array to keep track of the branches. (Hint: You’ll want to keep track of the branch directions and lengths by using vector math instead of p5.js transformations.) Can you animate the tree’s growth? What about drawing leaves at the ends of the branches?
The Stochastic Version
At first glance (and with the right angle), it may look like I’ve drawn a convincing tree in the previous example, but on closer inspection, the result is a little too perfect. Take a look outside at a real tree and you’ll notice that the branch lengths and angles vary from branch to branch, not to mention the fact that not all branches split off into exactly two smaller branches. Fractal trees are a great example of how adding a touch of randomness can make the end result look more natural. That bit of randomness also transforms the fractal from deterministic to stochastic—the exact outcome will be different from drawing to drawing, while still retaining the overall characteristics of a branching, tree-like structure.
First, how about randomizing the angle for each branch? This is a pretty easy one to do just by adding random():
let angle = random(0, PI / 3);
Pick a random angle from 0 to π/3 for each branch.
In the original example, branch() always calls itself twice. Now, for extra variety, I’ll instead pick a random number of branches (each with a random angle) for each branch.
Example 8.7: A Stochastic Tree
function branch(length) {
line(0, 0, 0, -length);
translate(0, -length);
length *= 0.67;
if (length > 2) {
let n = Math.floor(random(1, 4));
for (let i = 0; i < n; i++) {
A random number of branches
let angle = random(-PI / 2, PI / 2);
push();
rotate(angle);
branch(length);
pop();
A random angle
}
}
}
Example 8.7 demonstrates the use of randomness in angles and numbers of branches, but perhaps it goes too far: the resulting trees still don’t appear particularly organic. For a more natural-looking tree, you might try limiting the range of random angles more narrowly, or incorporating Perlin noise for more gradual angle changes.
Exercise 8.9
Set the angles of the tree branches according to Perlin noise values. Adjust the noise values over time to animate the tree. See if you can get it to appear as if it’s blowing in the wind.
Exercise 8.10
Use Toxiclibs.js to simulate tree physics. Each branch of the tree could be two particles connected with a spring. How can you get the tree to stand up and not fall down?
L-systems
In 1968, Hungarian botanist Aristid Lindenmayer developed a grammar-based system to model the growth patterns of plants. This system uses textual symbols and a specific set of rules to generate patterns, just as a language’s grammar defines rules for constructing sentences out of words. Known as an L-system (short for Lindenmayer system), this technique can be used to generate the recursive fractal patterns demonstrated so far in this chapter. L-systems are additionally valuable because they provide a mechanism for using simple symbols to keep track of fractal structures that require complex and multifaceted production rules.
Implementing an L-system in p5.js requires working with recursion, transformations, and strings of text. This chapter already covers recursion and transformations, but strings are new. Here’s a quick snippet of code demonstrating the three aspects of working with text important to L-systems: creating, concatenating, and iterating over strings. You can refer to the book’s website for additional string resources and tutorials.
let message1 = "Hello!";
A string is created as text between quotes (single or double).
let message2 = message1 + " Goodbye!";
Strings can be joined (concatenated) with the plus operator. The string is now "Hello Goodbye!"
for (let i = 0; i < message.length; i++) {
The length of a string is stored in its length property.
let character = message.charAt(i);
Individual characters can be accessed by an index, just like an array! I’m using charAt(i) instead of [i].
}
An L-system has three main components:
- Alphabet: An L-system’s alphabet comprises the valid characters that can be included. For example, I could say the alphabet is ABC, meaning that any valid “sentence” (a string of characters) in an L-system can include only these three characters.
- Axiom: The axiom is a sentence (created with characters from the alphabet) that describes the initial state of the system. For example, with the alphabet ABC, a possible axiom could be AAA, or B, or ACBAB.
- Rules: The production rules of an L-system describe ways of transforming the sentence. The rules are applied recursively, starting with the axiom, generating new sentences over and over again. An L-system rule includes two sentences, a predecessor and a successor. For example, the rule A → AB means that wherever an A (the predecessor) occurs in a sentence, it should be replaced with AB (the successor) in the next generation.
I’ll begin with a simple L-system. In fact, it’s Lindenmayer’s original L-system, which models the growth of algae. Here are its components:
| Alphabet | A, B |
| Axiom | A |
| Rules | A → AB B → A |
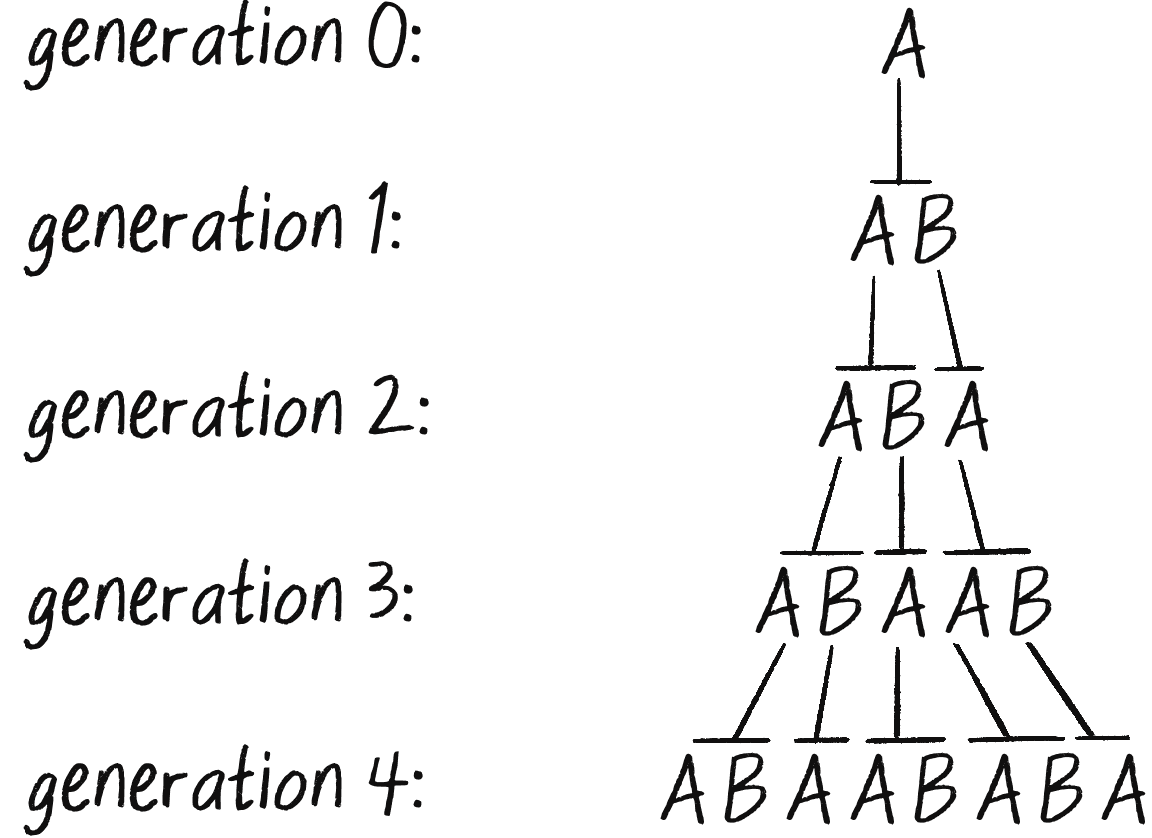
The L-system has an alphabet of two characters and features two simple rules: replace A with AB, and replace B with A. As with recursive fractal shapes, I can consider each successive application of the L-system rules to be a generation. Generation 0 is, by definition, the axiom (A), and each subsequent generation shows the result of applying the production rules to the current generation. Figure 8.20 shows several generations of this L-system’s development.
How can I implement this L-system with code? I’ll start by storing a string containing the axiom in a variable. I’ll name the variable current, as it will always store the current generation (starting with the axiom):
let current = "A";
Once again, just as with the Game of Life and the Koch curve, I now need an entirely separate string for the next generation:
let next = "";
Now it’s time to apply the production rules to current and write the results to next:
for (let i = 0; i < current.length; i++) {
let c = current.charAt(i);
if (c === "A") {
Production rule A → AB
next += "AB";
} else if (c === "B") {
Production rule B → A
next += "A";
}
}
When the for loop is done, current is set to next:
current = next;
To be sure this code is working, I’ll package it into a function called generate() and use a loop to call generate() multiple times, drawing the current string to the canvas.
Example 8.8: Simple L-system Sentence Generation
let current = "A";
Start with an axiom.
function setup() {
createCanvas(640, 160);
background(255);
noLoop();
for (let i = 0; i < 9; i++) {
generate();
Go through nine generations.
textSize(16);
textFont("courier");
text(i + ": " + current, 4, 20 + i * 16);
Render the text to the canvas.
}
}
function generate() {
let next = "";
for (let i = 0; i < current.length; i++) {
let c = current.charAt(i);
For every character of the current sentence . . .
if (c === "A") {
next += "AB";
} else if (c === "B") {
next += "A";
}
. . . apply the production rules A → AB, B → A.
}
current = next;
Save the next generation.
}
Right about now, you may be thinking, “This is all very interesting, but what exactly is the point? After all, isn’t this chapter supposed to be about drawing fractal patterns? I can see how the recursive nature of the L-system sentence structure relates to the recursive nature of fractals, but how exactly does this visually model plant growth? As far as I know, there aren’t any plants that sprout As and Bs.”
What I’ve left unsaid until now is that embedded into these L-system sentences are instructions for drawing, which is how Lindenmayer was able to translate strings of characters into the organic structures of plants. To see how this works, here’s another example system:
| Alphabet | A, B |
| Axiom | A |
| Rules | A → ABA B → BBB |
Here’s how this L-system plays out over a few generations:
| Generation 0 | A |
| Generation 1 | ABA |
| Generation 2 | ABABBBABA |
| Generation 3 | ABABBBABABBBBBBBBBABABBBABA |
To turn this into a drawing, I’ll translate the system’s alphabet in the following way:
| A | Draw a line forward. |
| B | Move forward (without drawing a line). |
Armed with this translation, I can treat each generation’s sentence as instructions for drawing. Figure 8.21 shows the result.

Look familiar? This L-system generated the Cantor set!
For simplicity, I’ve been using AB as an alphabet, but many L-systems use the characters F, G, +, –, [, and ] instead. Here’s what they mean:
| F | Draw a line and move forward. |
| G | Move forward (without drawing a line). |
| + | Turn right. |
| – | Turn left. |
| [ | Save current state. |
| ] | Restore current state. |
This type of drawing framework is often referred to as turtle graphics (from the old days of Logo programming). Imagine a turtle sitting on your p5.js canvas, able to accept a small set of commands: turn left, turn right, move forward, draw a line, and so on. While p5.js isn’t set up to operate this way by default, I can emulate a turtle graphics engine fairly easily with translate(), rotate(), and line(). Here’s how I would convert this L-system’s alphabet into p5.js code:
| F |
|
| G |
|
| + |
|
| – |
|
| [ |
|
| ] |
|
Assuming I’ve generated a sentence from the L-system, I can iterate through the sentence character by character and execute the appropriate code for each character:
for (let i = 0; i < sentence.length; i++) {
let c = sentence.charAt(i);
Look at each character one at a time.
if (c === 'F') {
line(0, 0, length, 0);
translate(length, 0);
} else if (c === 'G') {
translate(length, 0);
} else if (c === '+') {
rotate(angle);
} else if (c === '-') {
rotate(-anglee);
} else if (c === '[') {
push();
} else if (c === ']') {
pop();
}
Perform the correct task for each character.
This could also be written with a switch statement,
which might be nicer to look at, but leaving it as an
if...else statement helps readers unfamiliar with that syntax.
}
With this code and the right L-system conditions, I can draw incredibly elaborate, plantlike structures. For the next example, here’s the L-system I’ll use:
| Alphabet | F, G, +, –, [, ] |
| Axiom | F |
| Rules | F → FF + [+ F – F – F] – [– F + F + F] |
The sketch available for download on the book’s website takes all the L-system code provided in this section and organizes it into three elements:
rules: A JavaScript object that stores pairs of predecessor and successor strings for an L-system ruleLSystem: A class to iterate a new L-system generationTurtle: A class to manage reading the L-system sentence and following its instructions to draw on the screen
I won’t write out these classes here, since they simply duplicate the code I’ve already worked out in this chapter. Instead, I’ll show how all the elements come together in the main sketch.js file.
Example 8.9: An L-system
let lsystem;
let turtle;
function setup() {
createCanvas(640, 240);
let rules = {
"F": "FF+[+F-F-F]-[-F+F+F]",
};
Rules can be defined as a JavaScript object.
lsystem = new LSystem("F", rules);
The L-system is created with an axiom and a ruleset.
for (let i = 0; i < 4; i++) {
lsystem.generate();
}
Run the L-system through four generations.
turtle = new Turtle(4, radians(25));
}
The Turtle object has a length and angle.
function draw() {
background(255);
translate(width / 2, height);
Start at the bottom of the canvas.
turtle.render(lsystem.sentence);
Ask the turtle engine to render the sentence.
}
Throughout this book, I’ve extensively covered OOP in the context of classes such as Particle and p5.Vector. However, in Example 8.9, you may have noticed a shortcut I took when initializing the rules variable. Instead of defining a Rule class and invoking a constructor with the new keyword, I initialized the variable with a JavaScript object literal. With its key-value pairs, this is a convenient data structure for defining transformation rules for an L-system. Each key represents a character in the current generation that needs to be replaced (in this case, there’s just one, "F"), and that key’s value defines the replacement ("FF+[+F-F-F]-[-F+F+F]"). Although this example has only one rule, you could create additional rules as other key-value pairs in the object literal.
Exercise 8.11
Use an L-system as a set of instructions for creating objects stored in an array. Use trigonometry and vector math to perform the rotations instead of transformations (just as I did with the Koch curve in Example 8.5).
Exercise 8.12
The seminal work in L-systems and plant structures, The Algorithmic Beauty of Plants by Przemysław Prusinkiewicz and Aristid Lindenmayer (Springer), was published in 1990. Chapter 1 describes many sophisticated L-systems with additional drawing rules and available alphabet characters. It also describes several methods for generating stochastic L-systems. Expand the L-system code in Example 8.9 to include one or more of the extra features described by Prusinkiewicz and Lindenmayer.
Exercise 8.13
In this chapter, I emphasized using fractal algorithms for generating visual patterns. However, fractals can be found in other creative mediums. For example, they’re evident in Johann Sebastian Bach’s Cello Suite No. 3, and the structure of David Foster Wallace’s novel Infinite Jest (Little, Brown, 1996) was inspired by fractals. Consider using the examples in this chapter to generate audio or text.
The Ecosystem Project
Incorporate fractals into your ecosystem. Here are some possibilities:
- Add plantlike creatures to the ecosystem environment.
- Say one of your plants is similar to a fractal tree. Can you add leaves or flowers to the ends of the branches? What if the leaves can fall off the tree (depending on a wind force)? What if you add fruit that can be picked and eaten by the creatures?
- Design a creature with a fractal pattern.
- Use an L-system to generate instructions for the way a creature should move or behave.

 CODING TRAIN
CODING TRAIN


