Chapter 2: Forces
Don’t underestimate the Force.
—Darth Vader

Alexander Calder was a 20th-century American artist known for his kinetic sculptures that balance form and motion. His “constellations” were sculptures consisting of interconnected shapes and wire that demonstrate tension, balance, and the ever-present pull of gravitational attraction.
In the final example of Chapter 1, I demonstrated how to calculate a dynamic acceleration based on a vector pointing from a circle on the canvas to the mouse position. The resulting motion resembled a magnetic attraction between shape and mouse, as if a force was pulling the circle in toward the mouse. In this chapter, I’ll detail the concept of a force and its relationship to acceleration. The goal, by the end of this chapter, is to build a simple physics engine and understand how objects move around a canvas, responding to a variety of environmental forces.
A physics engine is a computer program (or code library) that simulates the behavior of objects in a physical environment. With a p5.js sketch, the objects are 2D shapes, and the environment is a rectangular canvas. Physics engines can be developed to be highly precise (requiring high-performance computing) or real time (using simple and fast algorithms). This chapter focuses on building a rudimentary physics engine, with an emphasis on speed and ease of understanding.
Forces and Newton’s Laws of Motion
Let’s begin by taking a conceptual look at what it means to be a force in the real world. Just like the word vector, the term force can have a variety of meanings. It can indicate a powerful physical intensity, as in “They pushed the boulder with great force,” or a powerful influence, as in “They’re a force to be reckoned with!” The definition of force that I’m interested in for this chapter is more formal and comes from Sir Isaac Newton’s three laws of motion:
A force is a vector that causes an object with mass to accelerate.
Hopefully, you recognize the first part of the definition: a force is a vector. Thank goodness you just spent a whole chapter learning what vectors are and how to program with them! I’ll start from there by explaining how Newton’s three laws of motion relate to what you already know about vectors; then I’ll illustrate the rest of the force definition as I go.
Newton’s First Law
Newton’s first law is commonly stated as follows:
An object at rest stays at rest, and an object in motion stays in motion.
However, this is missing an important element related to forces. I could expand the definition by stating:
An object at rest stays at rest, and an object in motion stays in motion, at a constant speed and direction unless acted upon by an unbalanced force.
When Newton came along, the prevailing theory of motion—formulated by Aristotle��—was nearly 2,000 years old. It stated that if an object is moving, some sort of force is required to keep it moving. Unless that moving thing is being pushed or pulled, it will slow down or stop. This theory was borne out through observation of the world. For example, if you toss a ball, it falls to the ground and eventually stops moving, seemingly because the force of the toss is no longer being applied.
This older theory, of course, isn’t true. As Newton established, in the absence of any forces, no force is required to keep an object moving. When an object (such as the aforementioned ball) is tossed in Earth’s atmosphere, its velocity changes because of unseen forces such as air resistance and gravity. An object’s velocity will remain constant only in the absence of any forces or only if the forces that act on it cancel each other out, meaning the net force adds up to zero. This is often referred to as equilibrium (see Figure 2.1). The falling ball will reach a terminal velocity (which stays constant) once the force of air resistance equals the force of gravity.
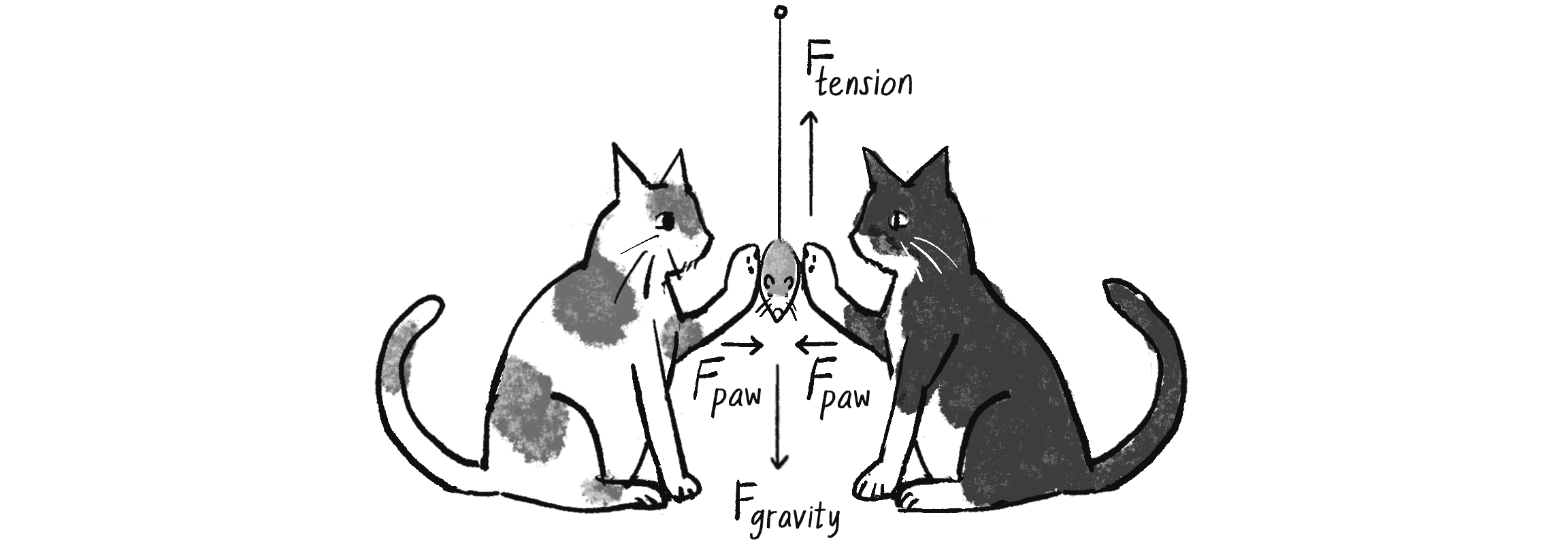
Considering a p5.js canvas, I could restate Newton’s first law as follows:
An object’s velocity vector will remain constant if it’s in a state of equilibrium.
In other words, in a Mover class, the update() function shouldn’t apply any mathematical operations on the velocity vector unless a nonzero net force is present.
Newton’s Third Law
Let me set aside Newton’s second law (arguably the most important law for the purposes of this book) for a moment and move on to his third law. This law is often stated as follows:
For every action, there is an equal and opposite reaction.
The way this law is stated frequently causes confusion. For one, it sounds like one force causes another. Yes, if you push someone, that someone may actively decide to push you back. But this isn’t the action and reaction Newton’s third law has in mind.
Let’s say you push against a wall. The wall doesn’t actively decide to push you back, and yet it still provides resistance with an equal force in the opposite direction. There’s no “origin” force. Your push simply includes both forces, referred to as an action/reaction pair. A better way of stating Newton’s third law might therefore be the following:
Forces always occur in pairs. The two forces are of equal strength but in opposite directions.
This still causes confusion because it sounds like these forces would always cancel each other out. This isn’t the case. Remember, the forces act on different objects. And just because the two forces are equal doesn’t mean that the objects’ movements are equal (or that the objects will stop moving).
Consider pushing on a stationary truck. Although the truck is far more massive than you, a stationary truck (unlike a moving one) will never overpower you and send you flying backward. The force your hands exert on the truck is equal and opposite to the force exerted by the truck on your hands. The outcome depends on a variety of other factors. If the truck is small and parked on an icy street, you’ll probably be able to get it to move. On the other hand, if it’s very large and on a dirt road and you push hard enough (maybe even take a running start), you could injure your hand.
And what if, as in Figure 2.2, you are wearing roller skates when you push on that truck?
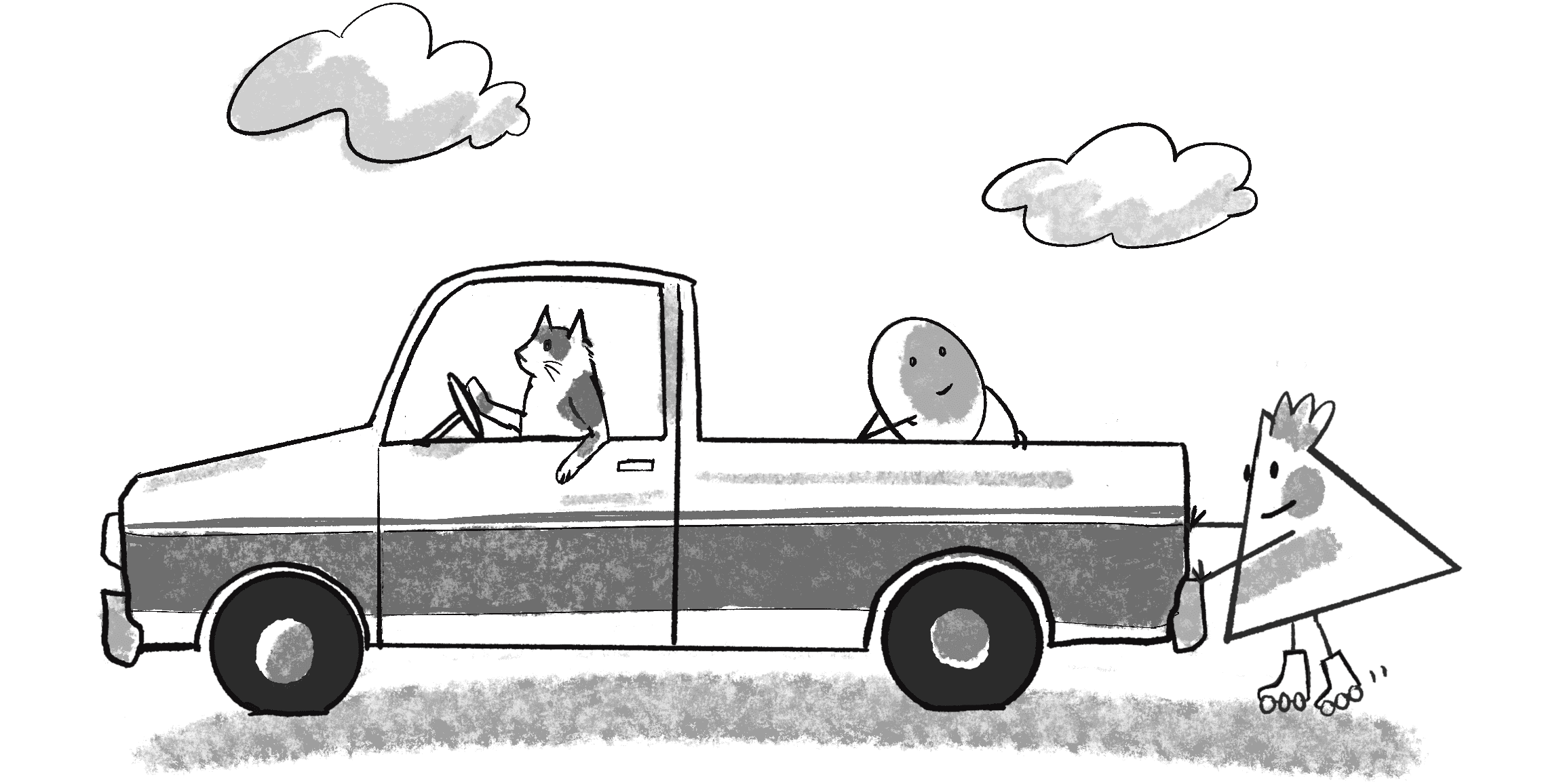
You’ll accelerate away from the truck, sliding along the road while the truck stays put. Why do you slide but not the truck? For one, the truck has a much larger mass (which I’ll get into with Newton’s second law). Other forces are at work too—namely, the friction of the truck’s tires and your roller skates against the road.
Considering p5.js again, I could restate Newton’s third law as follows:
If you calculate a p5.Vector called f that represents a force of object A on object B, you must also apply the opposite force that object B exerts on object A. You can calculate this other force as p5.Vector.mult(f, -1).
You’ll soon see that in the world of coding simulation, it’s often not necessary to stay true to Newton’s third law. Sometimes, such as in the case of gravitational attraction between bodies (see Example 2.8), I’ll want to model equal and opposite forces in my example code. Other times, such as a scenario where I’ll say, “Hey, there’s some wind in the environment,” I’m not going to bother to model the force that a body exerts back on the air. In fact, I’m not going to bother modeling the air at all! Remember, the examples in this book are taking inspiration from the physics of the natural world for the purposes of creativity and interactivity. They don’t require perfect precision.
Newton’s Second Law
Now it’s time for the most important law for you, the p5.js coder: Newton’s second law. It’s stated as follows:
Force equals mass times acceleration.
Or:
Why is this the most important law for this book? Well, let’s write it a different way:
Acceleration is directly proportional to force and inversely proportional to mass. Consider what this means if you’re pushed. The harder you’re pushed, the faster you’ll speed up or slow down (accelerate). On the other hand, the bigger you are, the less effective a force is at accelerating you!
Weight vs. Mass
Mass isn’t to be confused with weight. Mass is a measure of the amount of matter in an object (measured in kilograms). An object that has a mass of 1 kilogram on Earth would have a mass of 1 kilogram on the moon.
Weight, though often mistaken for mass, is technically the force of gravity on an object. From Newton’s second law, you can calculate weight as mass times the acceleration of gravity (). Weight is measured in newtons, a unit that indicates the magnitude of the gravitational force. Because weight is tied to gravity, an object on the moon weighs one-sixth as much as it does on Earth.
Related to mass is density, which is defined as the amount of mass per unit of volume (grams per cubic centimeter, for example).
In the world of p5.js, what is mass anyway? Aren’t we dealing with pixels? Let’s start simple and say that in a pretend pixel world, all objects have a mass equal to 1. Anything divided by 1 equals itself, and so, in this simple world, we have this:
I’ve effectively removed mass from the equation, making the acceleration of an object equal to force. This is great news. After all, Chapter 1 described acceleration as the key to controlling the movement of objects in a canvas. I said that the position changes according to the velocity, and the velocity according to acceleration. Acceleration seemed to be where it all began. Now you can see that force is truly where it all begins.
Let’s take the Mover class, with position, velocity, and acceleration:
class Mover {
constructor() {
this.position = createVector();
this.velocity = createVector();
this.acceleration = createVector();
}
}
Now the goal is to be able to add forces to this object, with code like this:
mover.applyForce(wind);
Or like this:
mover.applyForce(gravity);
Here wind and gravity are p5.Vector objects. According to Newton’s second law, I could implement this applyForce() method as follows:
applyForce(force) {
this.acceleration = force;
Newton’s second law at its simplest
}
This looks pretty good. After all, acceleration = force is a literal translation of Newton’s second law (in a world without mass). Nevertheless, this code has a pretty big problem, which I’ll quickly encounter when I return to my original goal: creating an object that responds to wind and gravity forces. Consider this code:
mover.applyForce(wind);
mover.applyForce(gravity);
mover.update();
Imagine you’re the computer for a moment. First, you call applyForce() with wind, and so the Mover object’s acceleration is now assigned the wind vector. Second, you call applyForce() with gravity. Now the Mover object’s acceleration is set to the gravity vector. Finally, you call update(). What happens in update()? Acceleration is added to velocity:
this.velocity.add(this.acceleration);
If you run this code, you won’t see an error in the console, but zoinks! There’s a major problem. What’s the value of acceleration when it’s added to velocity? It’s equal to the gravity vector, meaning wind has been left out! Anytime applyForce() is called, acceleration is overwritten. How can I handle more than one force?
Force Accumulation
The answer is that the forces must accumulate, or be added together. This is stated in the full definition of Newton’s second law itself, which I now confess to having simplified. Here’s a more accurate way to put it:
Net force equals mass times acceleration.
In other words, acceleration is equal to the sum of all forces divided by mass. At any given moment, there might be 1, 2, 6, 12, or 303 forces acting on an object. As long as the object knows how to add them together (accumulate them), it doesn’t matter how many forces there are. The sum total will give you the object’s acceleration (again, ignoring mass). This makes perfect sense. After all, as you saw in Newton’s first law, if all the forces acting on an object add up to zero, the object experiences an equilibrium state (that is, no acceleration).
I can now revise the applyForce() method to take force accumulation into account:
applyForce(force) {
this.acceleration.add(force);
Newton’s second law, but with force accumulation, adding all input forces to acceleration
}
I’m not finished just yet, though. Force accumulation has one more piece. Since I’m adding all the forces together at any given moment, I have to make sure that I clear acceleration (set it to 0) before each time update() is called. Consider a wind force for a moment. Sometimes wind is very strong, sometimes it��’s weak, and sometimes there’s no wind at all. For example, you might write code that creates a gust of wind when holding down the mouse:
if (mouseIsPressed) {
let wind = createVector(0.5, 0);
mover.applyForce(wind);
}
When the mouse is released, the wind should stop, and according to Newton’s first law, the object should continue moving at a constant velocity. However, if I forget to reset acceleration to 0, the gust of wind will still be in effect. Even worse, it will add onto itself from the previous frame! Acceleration, in a time-based physics simulation, has no memory; it’s calculated based on the environmental forces present at any given moment (frame) in time. This is different from, say, position. An object must remember its previous location in order to move properly to the next.
One way to clear the acceleration for each frame is to multiply the acceleration vector by 0 at the end of update():
update() {
this.velocity.add(this.acceleration);
this.position.add(this.velocity);
this.acceleration.mult(0);
Clear acceleration after it’s been applied.
}
Being able to accumulate and apply forces gets me closer to a working physics engine, but at this point I should note another detail that I’ve been glossing over, besides mass. That’s the time step, the rate at which the simulation updates. The size of the time step affects the accuracy and behavior of a simulation, which is why many physics engines incorporate the time step as a variable (often denoted as dt, which stands for delta time, or the change in time). For simplicity, I’m instead choosing to assume that every cycle through draw() represents one time step. This assumption may not be the most accurate, but it allows me to focus on the key principles of the simulation.
I’ll let this assumption stand until Chapter 6, when I’ll examine the impact of different time steps while covering third-party physics libraries. Right now, though, I can and should address the massive elephant in the room that I’ve so far been ignoring: mass.
Exercise 2.1
Using forces, simulate a helium-filled balloon floating upward and bouncing off the top of a window. Can you add a wind force that changes over time, perhaps according to Perlin noise?
Factoring In Mass
Newton’s second law is really , not . How can I incorporate mass into the simulation? To start, it’s as easy as adding a this.mass instance variable to the Mover class, but I need to spend a little more time here because of another impending complication.
First, though, I’ll add mass:
class Mover {
constructor() {
this.position = createVector();
this.velocity = createVector();
this.acceleration = createVector();
this.mass = ????;
Add mass as a number.
}
}
Units of Measurement
Now that I’m introducing mass, it’s important to make a quick note about units of measurement. In the real world, things are measured in specific units: two objects are 3 meters apart, the baseball is moving at a rate of 90 miles per hour, or this bowling ball has a mass of 6 kilograms. Sometimes you do want to take real-world units into consideration. In this chapter, however, I’m going to stick with units of measurement in pixels (“These two circles are 100 pixels apart”) and frames of animation (“This circle is moving at a rate of 2 pixels per frame,” the aforementioned time step).
In the case of mass, p5.js doesn’t have any unit of measurement to use. How much mass is in any given pixel? You might enjoy inventing your own p5.js unit of mass to associate with those values, like “10 pixeloids” or “10 yurkles.”
For demonstration purposes, I’ll tie mass to pixels (the larger a circle’s diameter, the larger the mass). This will allow me to visualize the mass of an object, albeit inaccurately. In the real world, size doesn’t indicate mass. A small metal ball could have a much higher mass than a large balloon because of its higher density. And for two circular objects with equal density, I’ll also note that mass should be tied to the formula for the area of a circle: . (This will be addressed in Exercise 2.11, and I’ll say more about and circles in Chapter 3.)
Mass is a scalar, not a vector, as it’s just one number describing the amount of matter in an object. I could get fancy and compute the area of a shape as its mass, but it’s simpler to begin by saying, “Hey, the mass of this object is . . . um, I dunno . . . how about 10?”
constructor() {
this.position = createVector(random(width), random(height));
this.velocity = createVector(0, 0);
this.acceleration = createVector(0, 0);
this.mass = 10;
}
This isn’t so great, since things become interesting only when I have objects with varying mass, but it’s enough to get us started. Where does mass come in? I need to divide force by mass to apply Newton’s second law to the object:
applyForce(force) {
force.div(this.mass);
this.acceleration.add(force);
Newton’s second law (with force accumulation and mass)
}
Yet again, even though the code looks quite reasonable, it has a major problem. Consider the following scenario with two Mover objects, both being blown away by a wind force:
let moverA = new Mover();
let moverB = new Mover();
let wind = createVector(1, 0);
moverA.applyForce(wind);
moverB.applyForce(wind);
Again, imagine you’re the computer. Object moverA receives the wind force—(1, 0)—divides it by mass (10), and adds it to acceleration:
| Action | Vector Components |
|---|---|
moverA receives the wind force. | (1, 0) |
moverA divides the wind force by a mass of 10. | (0.1, 0) |
Now you move on to object moverB. It also receives the wind force—(1, 0). Wait, hold on a second. What’s the value of the wind force? Taking a closer look, it’s actually now (0.1, 0)! Remember that when you pass an object (in this case, p5.Vector) into a function, you’re passing a reference to that object. It’s not a copy! So if a function makes a change to that object (which, in this case, it does by dividing by the mass), that object is permanently changed. But I don’t want moverB to receive a force divided by the mass of object moverA. I want it to receive the force in its original state—(1, 0). And so I must protect the original vector and make a copy of it before dividing by mass.
Fortunately, the p5.Vector class has a convenient method for making a copy: copy(). It returns a new p5.Vector object with the same data. And so I can revise applyForce() as follows:
applyForce(force) {
let f = force.copy();
Make a copy of the vector before using it.
f.div(this.mass);
Divide the copy by mass.
this.acceleration.add(f);
}
Let’s take a moment to recap what I’ve covered so far. I’ve defined what a force is (a vector), and I’ve shown how to apply a force to an object (divide it by mass and add it to the object’s acceleration vector). What’s missing? Well, I have yet to figure out how to calculate a force in the first place. Where do forces come from?
Exercise 2.2
You could write applyForce() in another way, using the static method div() instead of copy(). Rewrite applyForce() by using the static method. For help with this exercise, review static methods in “Static vs. Nonstatic Methods”.
applyForce(force) {
let f = p5.Vector.div(force, this.mass);
this.acceleration.add(f);
}
Creating Forces
This section presents two ways to create forces in a p5.js world:
- Make up a force! After all, you’re the programmer, the creator of your world. There’s no reason you can’t just make up a force and apply it.
- Model a force! Forces exist in the physical world, and physics textbooks often contain formulas for these forces. You can take these formulas and translate them into source code to model real-world forces in JavaScript.
To begin, I’ll focus on the first approach. The easiest way to make up a force is to just pick a number (or two numbers, really). Let’s start with simulating wind. How about a wind force that points to the right and is fairly weak? Assuming an object mover, the code would read as follows:
let wind = createVector(0.01, 0);
mover.applyForce(wind);
The result isn’t terribly interesting but is a good place to start. I create a p5.Vector object, initialize it, and pass it into a Mover object (which in turn will apply it to its own acceleration). To finish off this example, I’ll add one more force, gravity (pointing down), and engage the wind force only when the mouse is pressed.
Example 2.1: Forces
let gravity = createVector(0, 0.1);
mover.applyForce(gravity);
if (mouseIsPressed) {
let wind = createVector(0.1, 0);
mover.applyForce(wind);
}
Now I have two forces, pointing in different directions and with different magnitudes, both applied to the object mover. I’m beginning to get somewhere. I’ve built a world, an environment with forces that act on objects!
Let’s look at what happens now when I add a second object with a variable mass. To do this, you’ll probably want to do a quick review of OOP. Again, I’m not covering all the basics of programming here (for that, you can check out any of the intro p5.js books or video tutorials listed in “The Coding Train Connection”). However, since the idea of creating a world filled with objects is fundamental to all the examples in this book, it’s worth taking a moment to walk through the steps of going from one object to many.
This is where I left the Mover class. Notice that it’s identical to the Mover class created in Chapter 1, with two additions, mass and a new applyForce() method:
class Mover {
constructor() {
this.mass = 1;
For now, set the mass equal to 1 for simplicity.
this.position = createVector(width / 2, 30);
this.velocity = createVector(0, 0);
this.acceleration = createVector(0, 0);
}
applyForce(force) {
Newton’s second law
let f = p5.Vector.div(force, this.mass);
this.acceleration.add(f);
Receive a force, divide by mass, and add to acceleration.
}
update() {
this.velocity.add(this.acceleration);
this.position.add(this.velocity);
Motion 101 from Chapter 1
this.acceleration.mult(0);
Now add clearing the acceleration each time!
}
show() {
stroke(0);
fill(175);
circle(this.position.x, this.position.y, this.mass * 16);
Scale the size according to mass. Stay tuned for an improvement on this to come later in the chapter!
}
checkEdges() {
if (this.position.x > width) {
this.position.x = width;
this.velocity.x *= -1;
} else if (this.position.x < 0) {
this.velocity.x *= -1;
this.position.x = 0;
}
Somewhat arbitrarily, I’ve decided that an object bounces when it hits the edges of the canvas.
if (this.position.y > height) {
this.velocity.y *= -1;
this.position.y = height;
Even though I said not to touch position and velocity directly, exceptions exist. Here, I’m doing so as a quick way to reverse the direction of the object when it reaches the edge.
}
}
}
Now that the class is written, I can create more than one Mover object:
let moverA = new Mover();
let moverB = new Mover();
But there’s an issue. Look again at the Mover object’s constructor:
constructor() {
this.mass = 1;
this.position = createVector(width / 2, 30);
Every object has a mass of 1 and a position of (width / 2, 30).
this.velocity = createVector(0, 0);
this.acceleration = createVector(0, 0);
}
Right now, every Mover object is made exactly the same way. What I want are Mover objects of variable mass that start at variable positions. A nice way to accomplish this is with constructor arguments:
constructor(x, y, mass) {
this.mass = mass;
this.position = createVector(x, y);
Now set these variables with arguments.
this.velocity = createVector(0, 0);
this.acceleration = createVector(0, 0);
}
Notice that the mass and position are no longer set to hardcoded numbers, but rather are initialized via the x, y, and mass arguments passed to the constructor. This means I can create a variety of Mover objects—big ones, small ones, ones that start on the left side of the canvas, ones that start on the right, and everywhere in between:
let moverA = new Mover(100, 30, 10);
A large mover on the left side of the canvas
let moverB = new Mover(400, 30, 2);
A smaller mover on the right side of the canvas
I could choose to initialize the values in all sorts of ways (random, Perlin noise, in a grid, and so on). Here I’ve just picked some numbers for demonstration purposes. I’ll introduce other techniques for initializing a simulation throughout this book.
Once the objects are declared and initialized, the rest of the code follows as before. For each object, pass the forces in the environment to applyForce() and enjoy the show!
Example 2.2: Forces Acting on Two Objects
function draw() {
background(255);
let gravity = createVector(0, 0.1);
moverA.applyForce(gravity);
moverB.applyForce(gravity);
Make up a gravity force and apply it.
if (mouseIsPressed) {
let wind = createVector(0.1, 0);
moverA.applyForce(wind);
moverB.applyForce(wind);
}
Make up a wind force and apply it when the mouse is clicked.
moverA.checkEdges();
moverA.update();
moverA.show();
moverB.checkEdges();
moverB.update();
moverB.show();
}
Notice that every operation in the code is written twice, once for moverA and once for moverB. In practice, an array would make more sense than separate variables to manage multiple Mover objects, particularly as their number increases. That way, I’d have to write each operation only once and use a loop to apply it to each Mover in the array. I’ll demonstrate this later in the chapter and cover arrays in greater detail in Chapter 4.
Exercise 2.3
Instead of objects bouncing off the edge of the wall, create an example that includes an invisible force pushing back on the objects to keep them in the window. Can you weight the force according to the object’s distance from an edge so that the closer it is, the stronger the force?
Exercise 2.4
Fix the bouncing off the sides of the canvas so that the circle changes direction when its edge hits the side, rather than its center.
Exercise 2.5
Create a wind force that’s variable. Can you make it interactive? For example, think of a fan located where the mouse is and pointed toward the circles.
When you run the code in Example 2.2, notice that the small circle responds more dramatically to the forces applied to it than the large one. This is because of the formula acceleration = force divided by mass. Mass is in the denominator, so the larger it is, the smaller the acceleration. This makes sense for the wind force—the more massive an object, the harder it should be for the wind to push it around—but is it accurate for a simulation of Earth’s gravitational pull?
If you were to climb to the top of the Leaning Tower of Pisa and drop two balls of different masses, which one would hit the ground first? According to legend, Galileo performed this exact test in 1589, discovering that they fell with the same acceleration, hitting the ground at the same time. Why? I’ll dive deeper into this shortly, but the quick answer is that even though the force of gravity is calculated relative to an object’s mass—so that the bigger the object, the stronger the force—that force is canceled out when you divide by the mass to determine the acceleration. Therefore, the acceleration of gravity for different objects is equal.
A quick fix to the sketch—one that moves a step closer to realistically modeling a force rather than simply making up a force—is to implement this scaling by multiplying the gravity force by mass.
Example 2.3: Gravity Scaled by Mass
let gravity = createVector(0, 0.1);
Made-up gravity force
let gravityA = p5.Vector.mult(gravity, moverA.mass);
moverA.applyForce(gravityA);
Scale by mover A’s mass.
let gravityB = p5.Vector.mult(gravity, moverB.mass);
moverB.applyForce(gravityB);
Scale by mover B’s mass.
The objects now fall at the same rate. I’m still basically making up the gravity force by arbitrarily setting it to 0.1, but by scaling the force according to the object’s mass, I’m making it up in a way that’s a little truer to Earth’s actual force of gravitational attraction. Meanwhile, because the strength of the wind force is independent of mass, the smaller circle still accelerates to the right more quickly when the mouse is pressed. (The online code for this example also includes a solution to Exercise 2.4, with the addition of a radius variable in the Mover class.)
Modeling a Force
Making up forces will actually get you quite far—after all, I just made up a pretty good approximation of Earth’s gravity. Ultimately, the world of p5.js is an orchestra of pixels, and you’re the conductor, so whatever you deem appropriate to be a force, well by golly, that’s the force it should be! Nevertheless, there may come a time when you find yourself wondering, “But how does it all really work?” That’s when modeling forces, instead of just making them up, enters the picture.
Parsing Formulas
In a moment, I’m going to write out the formula for friction. This won’t be the first time you’ve seen a formula in this book; I just finished up the discussion of Newton’s second law, (or force equals mass times acceleration). You hopefully didn’t spend a lot of time worrying about that formula, because it’s just a few characters and symbols. Nevertheless, it’s a scary world out there. Just take a look at the equation for a normal distribution, which I covered (without presenting the formula) in “A Normal Distribution of Random Numbers”:
Formulas are regularly written with many symbols (often with letters from the Greek alphabet). Here’s the formula for friction (as indicated by ):
If it’s been a while since you’ve looked at a formula from a math or physics textbook, three key points are important to cover before I move on:
- Evaluate the right side; assign to the left side. This is just like in code! In the preceding case, the left side represents what I want to calculate—the force of friction—and the right side elaborates on how to do it.
- Am I talking about a vector or a scalar? It’s important to realize that in some cases, you’ll be calculating a vector; in others, a scalar. For example, in this case, the force of friction is a vector. That is indicated by the arrow above the . It has a magnitude and direction. The right side of the equation also has a vector, as indicated by the symbol , which in this case stands for the velocity unit vector.
- When symbols are placed next to each other, this typically means multiply them. The right side of the friction formula has four elements: –, μ, N, and . They should be multiplied together, reading the formula as .
Open up any high school physics textbook and you’ll find diagrams and formulas describing various forces—gravity, electromagnetism, friction, tension, elasticity, and more. For the rest of this chapter, I’m going to consider three forces—friction, drag, and gravitational attraction—and show how to model them with p5.js. The point I’d like to make here is not that these are fundamental forces that you always need in your simulations. Rather, I want to demonstrate these forces as case studies for the following process:
- Understanding the concept behind a force
- Deconstructing the force’s formula into two parts:
- How do you compute the force’s direction?
- How do you compute the force’s magnitude?
- Translating that formula into p5.js code that calculates a vector to be passed through a
Moverobject’sapplyForce()method
If you can follow these steps with the example forces I’ll provide here, then hopefully when you find yourself googling atomic nuclei weak nuclear force at 3 AM, you’ll have the skills to take what you find and adapt it for p5.js.
Friction
Let’s begin with friction and follow the preceding steps. Whenever two surfaces come into contact, they experience friction. Friction is a dissipative force, meaning it causes the kinetic energy of an object to be converted into another form, giving the impression of loss, or dissipation.
Let’s say you’re driving a car. When you press your foot on the brake pedal, the car’s brakes use friction to slow the motion of the tires. Kinetic energy (motion) is converted into thermal energy (heat). A complete model of friction would include separate cases for static friction (a body at rest against a surface) and kinetic friction (a body in motion against a surface), but for simplicity here, I’m going to work through only the kinetic case. Figure 2.3 shows the formula for friction.
Since friction is a vector, let me separate this formula into two parts that determine the direction of friction as well as its magnitude. Figure 2.3 indicates that friction points in the opposite direction of velocity. In fact, that’s the part of the formula that says , or –1 times the velocity unit vector. In p5.js, this would mean taking an object’s velocity vector and multiplying it by -1:
let friction = this.velocity.copy();
friction.normalize();
friction.mult(-1);
Let’s figure out the direction of the friction force (a unit vector in the opposite direction of velocity).
Notice two additional steps here. First, it’s important to make a copy of the velocity vector, as I don’t want to reverse the object’s direction by accident. Second, the vector is normalized. This is because the magnitude of friction isn’t associated with the speed of the object, and I want to start with a vector of length 1 so it can easily be scaled.
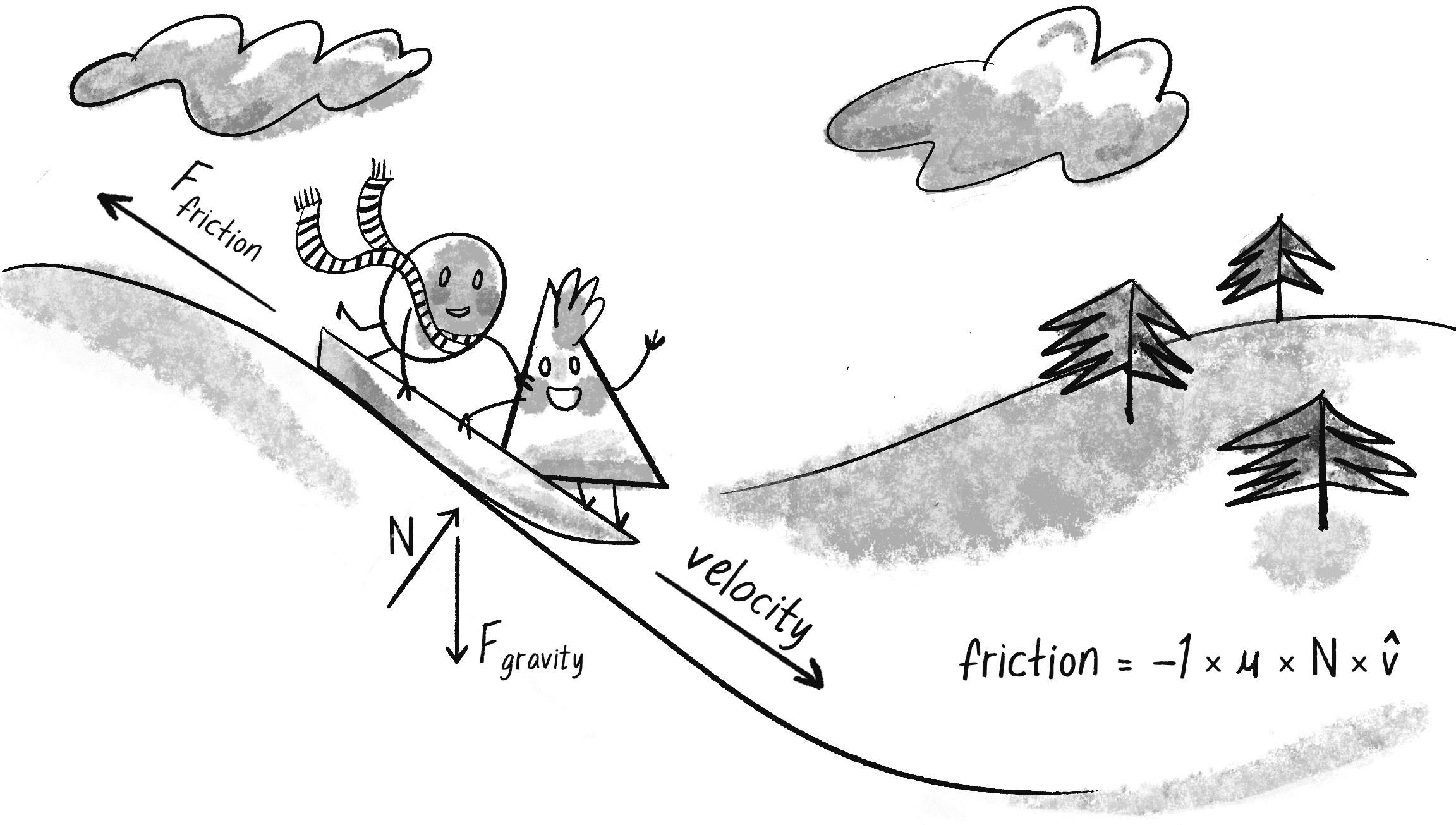
According to the formula, the magnitude is . The Greek letter mu (, pronounced mew) is used here to describe the coefficient of friction. The coefficient of friction establishes the strength of a friction force for a particular surface. The higher it is, the stronger the friction; the lower, the weaker. A block of ice, for example, will have a much lower coefficient of friction than, say, sandpaper. Since this is a pretend p5.js world, I can arbitrarily set the coefficient to scale the strength of the friction:
let c = 0.01;
Now for the second part. N refers to the normal force, the force perpendicular to the object’s motion along a surface. Think of a vehicle driving along a road. The vehicle pushes down against the road with gravity, and Newton’s third law tells us that the road, in turn, pushes back against the vehicle. That’s the normal force. The greater the gravitational force, the greater the normal force.
As you’ll see in the next section, gravitational attraction is associated with mass, and so a lightweight sports car would experience less friction than a massive tractor trailer truck. In Figure 2.3, however, because the object is moving along a surface at an angle, computing the magnitude and direction of the normal force is a bit more complex because it doesn’t point in the opposite direction of gravity. You’d need to know something about angles and trigonometry.
All of these specifics are important; however, a “good enough” simulation can be achieved without them. I can, for example, make friction work with the assumption that the normal force will always have a magnitude of 1. When I get into trigonometry in the next chapter, you could return to this question and make the friction example more sophisticated. And so:
let normal = 1;
Now that I have the magnitude and direction for friction, I can put it all together in code:
let c = 0.1;
let normal = 1;
let frictionMag = c * normal;
Calculate the magnitude of friction (really just an arbitrary constant).
let friction = mover.velocity.copy();
friction.mult(-1);
friction.normalize();
friction.mult(frictionMag);
Take the unit vector and multiply it by the magnitude. This is the force vector!
This code calculates a friction force but doesn’t answer the question of when to apply it. There’s no answer to this question, of course, given this is all a made-up world visualized in a 2D p5.js canvas! I’ll make the arbitrary, but logical, decision to apply friction when the circle comes into contact with the bottom of the canvas, which I can detect by adding a function to the Mover class, called contactEdge():
contactEdge() {
return (this.position.y > height - this.radius - 1);
The mover is touching the edge when it’s within 1 pixel.
}
This is a good time for me to also mention that the actual bouncing off the edge here simulates an idealized elastic collision, meaning no kinetic energy is lost when the circle and the edge collide. This is rarely true in the real world; pick up a tennis ball and drop it against any surface, and the height at which it bounces will slowly lower until it rests against the ground. Many factors are at play here (including air resistance, which I’ll cover in the next section), but a quick way to simulate an inelastic collision is to reduce the magnitude of velocity by a percentage with each bounce:
bounceEdges() {
let bounce = -0.9;
A new variable to simulate an inelastic collision: 10% of the velocity’s x- or y-component is lost.
if (this.position.y > height - this.radius) {
this.position.y = height - this.radius;
this.velocity.y *= bounce;
}
}
Finally, I can add all these pieces to the code from Example 2.3 and simulate the object experiencing three forces: wind (when the mouse is clicked), gravity (always), and now friction (when in contact with the bottom of the canvas).
Example 2.4: Including Friction
function draw() {
background(255);
let gravity = createVector(0, 1);
mover.applyForce(gravity);
I should scale by mass to be more accurate, but this example has only one circle.
if (mouseIsPressed) {
let wind = createVector(0.5, 0);
mover.applyForce(wind);
}
if (mover.contactEdge()) {
let c = 0.1;
let friction = mover.velocity.copy();
friction.mult(-1);
friction.setMag(c);
mover.applyForce(friction);
Apply the friction force vector to the object.
}
mover.bounceEdges();
Call the new bounceEdges() method.
mover.update();
mover.show();
}
Running this example, you’ll notice that the circle eventually comes to rest. You can make this happen more or less quickly by varying the coefficient of friction as well as the percentage of speed lost in the bounceEdges() method.
Exercise 2.6
Add a second object to Example 2.4. How do you handle having two objects of different masses? What if each object has its own coefficient of friction relative to the bottom surface? Does it make sense to encapsulate the friction force calculation into a Mover method?
Exercise 2.7
Instead of wind, can you add functionality to this example that allows you to toss the circle via mouse interaction?
Air and Fluid Resistance
Friction also occurs when a body passes through a liquid or gas. The resulting force has many names, all really meaning the same thing: viscous force, drag force, air resistance, or fluid resistance (see Figure 2.4).
The effect of a drag force is ultimately the same as the effect in our previous friction examples: the object slows down. The exact behavior and calculation of a drag force is a bit different, however. Here’s the formula:
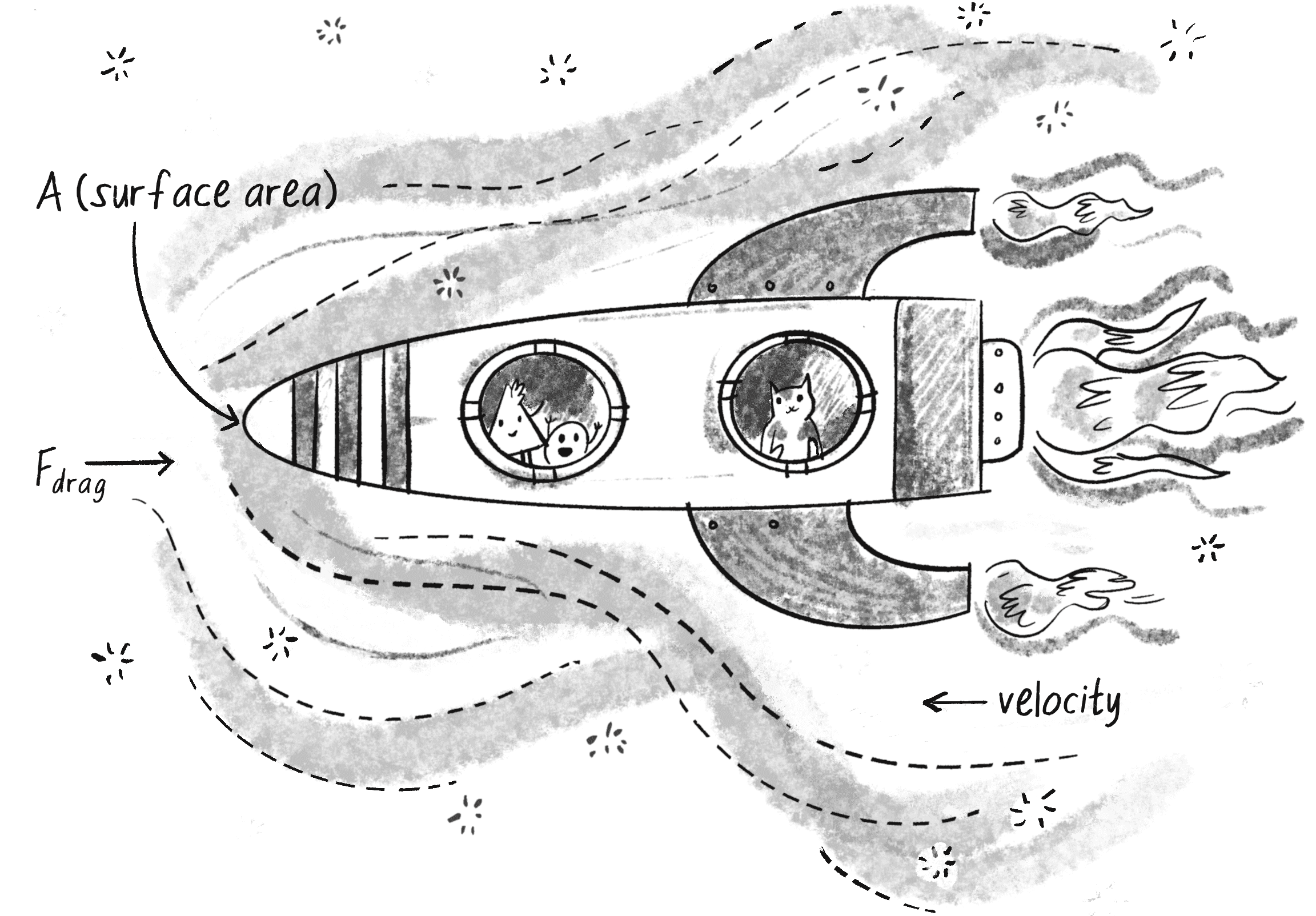
Let me break this down to see what’s really necessary for an effective simulation in p5.js, making a simpler formula in the process:
- refers to drag force, the vector to compute and pass into the
applyForce()method. - –1/2 is a constant: –0.5. While it’s an important factor to scale the force, it’s not terribly relevant here, as I’ll be making up values for other scaling constants. However, the fact that it’s negative is important, as it indicates that the force points in the opposite direction of velocity (just as with friction).
- is the Greek letter rho, another constant that refers to the density of the liquid. I’ll choose to ignore this at the moment and consider it to have a constant value of 1.
- refers to the speed of the moving object. Okay, you’ve got this one! The object’s speed is the magnitude of the velocity vector:
velocity.mag(). And just means squared, or . (I’ll note that this assumes the liquid or gas is stationary and not moving; if you drop an object into a flowing river, you’d have to also take the relative speed of the water into account.) - refers to the frontal surface area of the object that’s pushing through the liquid or gas. Consider a flat sheet of paper falling through the air and compare it to a sharp pencil pointed straight down. The pencil will experience less drag because it has less surface area pointing in its direction of motion. Again, this is a constant, and to keep the implementation simple, I’ll consider all objects to have a spherical shape and ignore this element.
- is the coefficient of drag, exactly the same as the coefficient of friction (μ). This constant will determine the relative strength of the drag force.
- should look familiar. It’s the velocity unit vector, found with
velocity.normalize(). Just like friction, drag is a force that points in the opposite direction of velocity.
Now that I’ve analyzed each of these parts and determined what’s needed for my simulation, I can reduce the formula, as shown in Figure 2.5.
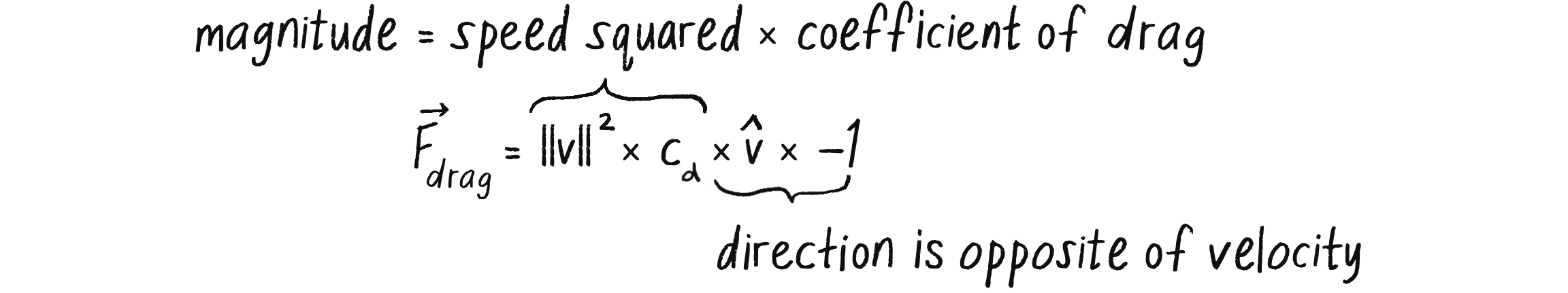
While I’ve written the simplified formula with as the lone constant representing the coefficient of drag, I can also think of it as all the constants combined (, , ). A more sophisticated simulation might treat these constants separately; you could try factoring them in as an exercise.
Here’s the p5.js version of the simplified drag formula:
let c = 0.1;
let speed = this.velocity.mag();
let dragMagnitude = c * speed * speed;
Part 1 of the formula (magnitude)
let drag = this.velocity.copy();
drag.mult(-1);
Part 2 of the formula (direction)
drag.setMag(dragMagnitude);
Magnitude and direction together!
Let’s implement this force in the Mover example. But when should I apply it? Earlier, I enabled the friction force to slow the mover whenever it came into contact with the bottom edge of the canvas. Now, I’ll introduce a new element to the environment: a Liquid object that exerts a drag force when the mover passes through it. The “liquid” will be drawn as a rectangle, with position, width, and height, and will have a coefficient of drag that sets whether it’s easy for objects to move through it (like air) or difficult (like molasses). In addition, Liquid will include a show() method so we can see the liquid on the canvas:
class Liquid {
constructor(x, y, w, h, c) {
this.x = x;
this.y = y;
this.w = w;
this.h = h;
this.c = c;
The Liquid object includes a variable defining its coefficient of drag.
}
show() {
noStroke();
fill(175);
rect(this.x, this.y, this.w, this.h);
}
}
Now the sketch needs a liquid variable, initialized in setup(). I’ll place the liquid in the bottom half of the canvas:
let liquid;
function setup() {
liquid = new Liquid(0, height / 2, width, height / 2, 0.1);
Initialize a Liquid object. I’m choosing a low coefficient (0.1) for a weaker effect. Try a stronger one!
}
Now comes an interesting question: How does the Mover object talk to the Liquid object? I want to implement the following:
When a mover passes through a liquid, that mover experiences a drag force.
Translating that into object-oriented speak:
if (liquid.contains(mover)) {
let dragForce = liquid.calculateDrag(mover);
mover.applyForce(dragForce);
}
If the liquid contains the mover, apply the drag force.
This code serves as instructions for what I need to add to the Liquid class: (1) a contains() method that determines whether a Mover object is inside the Liquid object’s area, and (2) a drag() method that calculates and returns the appropriate drag force to be applied to the Mover.
The first is easy; I can use a Boolean expression to determine whether the position vector rests inside the rectangle defined by the liquid:
contains(mover) {
let pos = mover.position;
Store position in a separate variable to make the code more readable.
return (pos.x > this.x && pos.x < this.x + this.w &&
pos.y > this.y && pos.y < this.y + this.h);
This Boolean expression determines whether the position vector is contained within the rectangle defined by the Liquid class.
}
The calculateDrag() method is pretty easy too: I basically already wrote the code for it when I implemented the simplified drag formula! The drag force is equal to the coefficient of drag multiplied by the speed of the mover squared, in the opposite direction of velocity:
calculateDrag(mover) {
let speed = mover.velocity.mag();
let dragMagnitude = this.c * speed * speed;
Calculate the force’s magnitude.
let dragForce = mover.velocity.copy();
dragForce.mult(-1);
Calculate the force’s direction.
dragForce.setMag(dragMagnitude);
Finalize the force: set the magnitude and direction together.
return dragForce;
Return the force.
}
With these two methods added to the Liquid class, I’m ready to put all the code together! In the following example, I’ll expand the code to use an array of evenly spaced Mover objects in order to demonstrate how the drag force behaves with objects of variable mass. This also illustrates an alternate way to initialize a simulation other than randomly. Look for 40 + i * 70 in the code. An initial offset of 40 provides a small margin from the edge of the canvas, and i * 70 uses the index of the object to evenly space the movers. The margin and multiplier are arbitrary; you might try other values or consider other ways to calculate the spacing based on the canvas dimensions.
Example 2.5: Fluid Resistance
let movers = [];
let liquid;
function setup() {
createCanvas(640, 240);
for (let i = 0; i < 9; i++) {
Initialize an array of Mover objects.
let mass = random(0.1, 5);
Use a random mass for each one.
movers[i] = new Mover(40 + i * 70, 0, mass);
The x-values are spaced out evenly according to i.
}
liquid = new Liquid(0, height / 2, width, height / 2, 0.1);
}
function draw() {
background(255);
liquid.show();
Draw the liquid.
for (let i = 0; i < movers.length; i++) {
if (liquid.contains(movers[i])) {
Is the mover in the liquid?
let dragForce = liquid.drag(movers[i]);
Calculate the drag force.
movers[i].applyForce(dragForce);
Apply the drag force to the mover.
}
let gravity = createVector(0, 0.1 * movers[i].mass);
Gravity is scaled by mass here!
movers[i].applyForce(gravity);
Apply gravity.
movers[i].update();
movers[i].show();
movers[i].checkEdges();
Update and display the mover.
}
}
Running the example, you may notice that it appears to simulate objects falling into water. The objects slow down only when crossing through the gray area at the bottom of the window (representing the liquid). You’ll also notice that the smaller objects slow down a great deal more than the larger objects. Remember Newton’s second law? Acceleration equals force divided by mass (), so a massive object will accelerate less, and a smaller object will accelerate more. In this case, the acceleration is the slowing down due to drag. The smaller objects slow down at a greater rate than the larger ones.
Exercise 2.8
You might notice that if you set the coefficient of drag too high in Example 2.5, the circles may bounce off of the liquid! This is due to the inaccuracy of the large time steps that I mentioned earlier in this chapter. A drag force will cause an object to stop but never to reverse direction. How can you use the vector limit() method to correct this issue? You might also try dropping the objects from variable heights. How does this affect the drag as they hit the liquid?
Exercise 2.9
The original formula for drag included surface area. Can you create a simulation of boxes falling into water with a drag force dependent on the length of the side hitting the water?
Exercise 2.10
In addition to drag being a force in opposition to the velocity vector, a drag force can be perpendicular. Known as lift-induced drag, this will cause an airplane with an angled wing to rise in altitude. Try creating a simulation of lift.
Gravitational Attraction
Probably the most famous force of all is gravitational attraction. We humans on Earth think of gravity as stuff falling down, like an apple hitting Sir Isaac Newton on the head. But this is only our experience of gravity. The reality is more complicated.
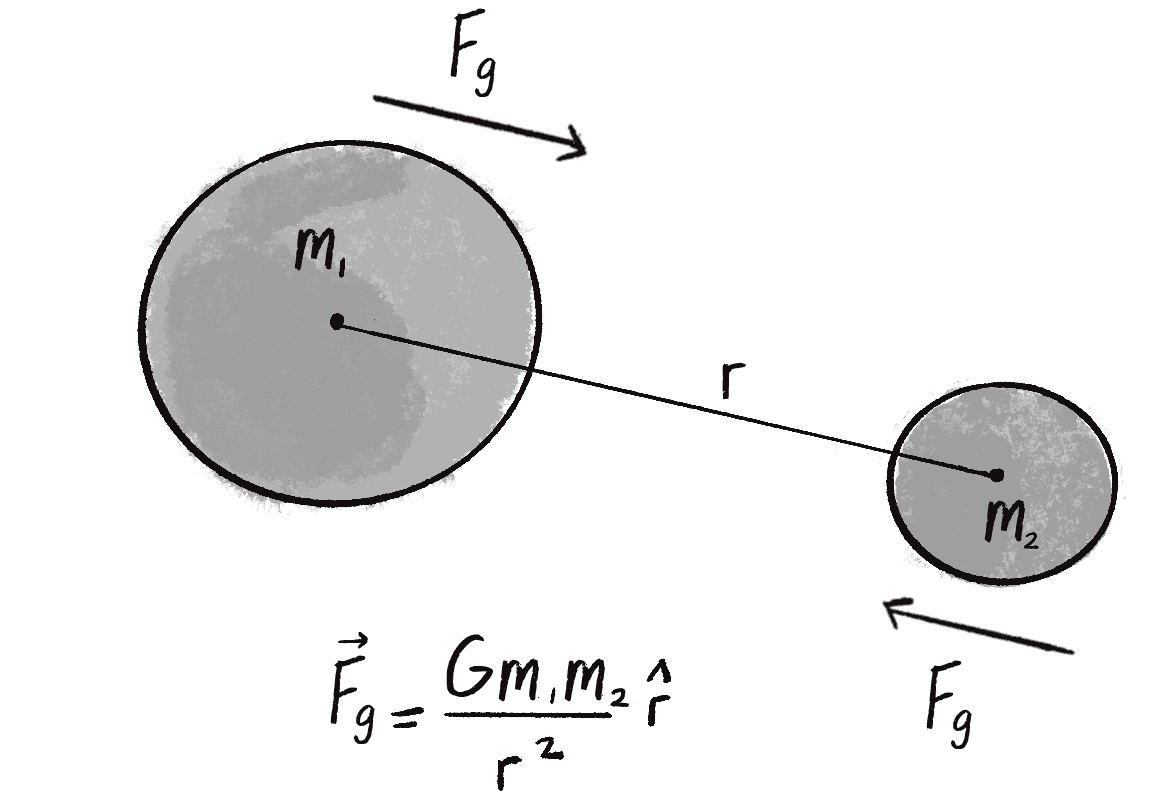
In truth, just as Earth pulls the apple toward it because of a gravitational force, the apple pulls Earth as well (this is Newton’s third law). Earth is just so freaking massive that it overwhelms all the other gravity interactions. In fact, every object with mass exerts a gravitational force on every other object. The formula for calculating the strengths of these forces is depicted in Figure 2.6.
Let’s examine this formula a bit more closely:
- refers to the gravitational force, the vector to compute and pass into the
applyForce()method. - is the universal gravitational constant, which in our world equals meters cubed per kilogram per second squared. This is a pretty important number if you’re a human being, but it’s not so important if you’re a shape wandering around a p5.js canvas. Again, it’s a constant that can be used to scale the forces in the world, making them stronger or weaker. Just setting it equal to 1 and ignoring it isn’t such a terrible choice either.
- and are the masses of objects 1 and 2. As I initially did with Newton’s second law (), mass is also something I could choose to ignore. After all, shapes drawn onscreen don’t have a physical mass. However, if you keep track of this value, you can create more interesting simulations in which “bigger” objects exert a stronger gravitational force than “smaller” ones.
- refers to the unit vector pointing from object 1 to object 2. As you’ll see in a moment, this direction vector can be computed by subtracting the position of one object from the other.
- is the distance between the two objects squared.
Take a moment to think about this formula. With everything on the top of the formula—, , —the bigger its value, the stronger the force. Big mass, big force. Big , big force. For on the bottom, however, it’s the opposite: the bigger the value (the farther away the object), the weaker the force. Mathematically, the strength of the gravitational force is inversely proportional to the distance squared.
Now it’s time to figure out how to translate this formula into p5.js code. For that, I’ll make the following assumptions:
- There are two objects.
- Each object has a position:
position1andposition2. - Each object has a mass:
mass1andmass2. - The variable
Grepresents the universal gravitational constant.
Given these assumptions, I want to compute a vector, the force of gravity. I’ll do it in two parts. First, I’ll compute the direction of the force ( in the formula). Second, I’ll calculate the strength of the force according to the masses and distance.
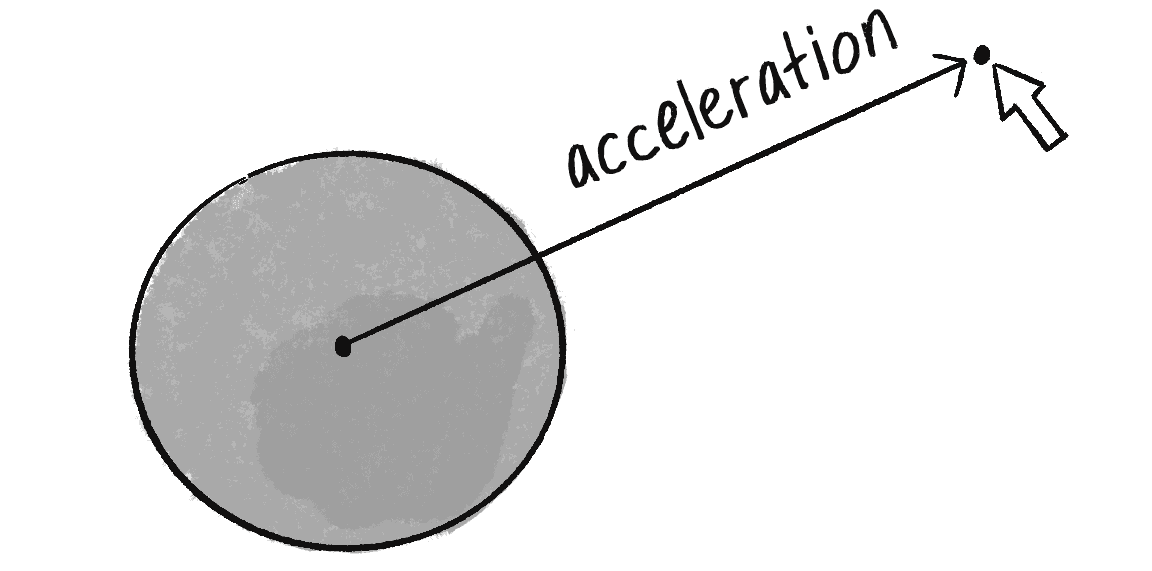
Remember in Chapter 1, when I created an object accelerating toward the mouse (see Figure 2.7)? As I showed then, a vector can be thought of as the difference between two points, so to calculate a vector pointing from the circle to the mouse, I subtracted one point from another:
let direction = p5.Vector.sub(mouse, position);
Now I can do the same thing to calculate . The direction of the attraction force that object 1 exerts on object 2 is equal to the following:
let direction = p5.Vector.sub(position1, position2);
direction.normalize();
Don’t forget that since I want a unit vector, a vector that indicates direction only, it’s important to normalize the vector after subtracting the positions. (Later, I might skip this step and use setMag() instead.)
Now that I have the direction of the force, I need to compute its magnitude and scale the vector accordingly:
let magnitude = (G * mass1 * mass2) / (distance * distance);
dir.mult(magnitude);
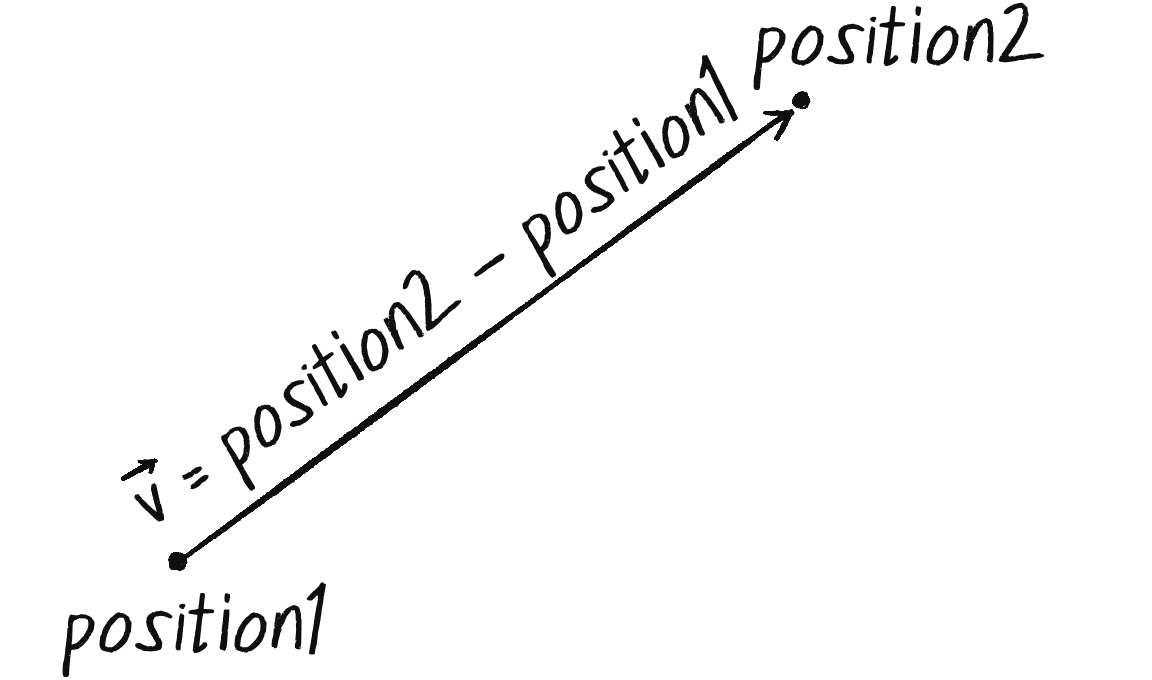
The only problem is that I don’t know the distance. The values of G, mass1, and mass2 are all givens, but I need to calculate distance before the preceding code will work. But wait, didn’t I just make a vector that points all the way from one object’s position to the other? The length of that vector should be the distance between the two objects (see Figure 2.8).
Indeed, if I add one more line of code and grab the magnitude of that vector before normalizing it, I’ll have the distance. And this time, I’ll skip the normalize() step and use setMag():
let force = p5.Vector.sub(position2, position1);
The vector that points from one object to another
let distance = force.mag();
The length (magnitude) of that vector is the distance between the two objects.
let magnitude = (G * mass1 * mass2) / (distance * distance);
Use the formula for gravity to compute the strength of the force.
force.setMag(magnitude);
Normalize and scale the force vector to the appropriate magnitude.
Note that I also changed the name of the direction vector to force. After all, when the calculations are finished, the vector I started with ends up being the actual force vector I wanted all along.
Now that I’ve worked out the math and code for calculating an attractive force (emulating gravitational attraction), let’s turn our attention to applying this technique in the context of an actual p5.js sketch. I’ll continue to use the Mover class as a starting point—a template for making objects with position, velocity, and acceleration vectors, as well as an applyForce() method. I’ll take this class and put it in a sketch with the following:
- A single
Moverobject - A single
Attractorobject (a new class that will have a fixed position)
The Mover object will experience a gravitational pull toward the Attractor object, as illustrated in Figure 2.9.
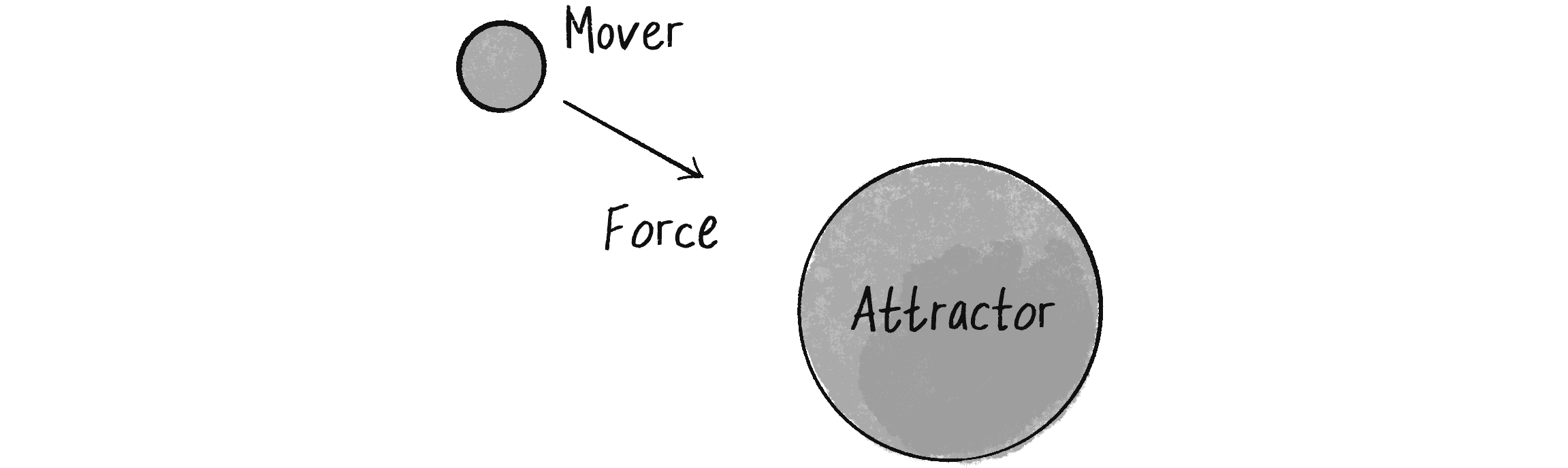
I’ll start by creating a basic Attractor class, giving it a position and a mass, along with a method to draw itself (tying mass to size):
class Attractor {
constructor() {
this.position = createVector(width / 2, height / 2);
this.mass = 20;
The attractor is an object that doesn’t move. It needs just a mass and a position.
}
show() {
stroke(0);
fill(175, 200);
circle(this.position.x, this.position.y, this.mass * 2);
}
}
In the sketch, I’ll add a variable to hold an object instance of the Attractor:
let mover;
let attractor;
function setup() {
createCanvas(640, 360);
mover = new Mover(300, 100, 5);
attractor = new Attractor();
Initialize the Attractor object.
}
function draw() {
background(255);
attractor.show();
Draw the Attractor object.
mover.update();
mover.show();
}
This is a good start: a sketch with a Mover object and an Attractor object, made from classes that handle the variables and behaviors of movers and attractors. The last piece of the puzzle is getting one object to attract the other. How do these two objects communicate? This could be done in various ways. Here are just some of the possibilities:
| Task | Function |
|---|---|
|
|
|
|
|
|
|
|
It’s good to consider a range of options, and you could probably make arguments for each of these approaches. I’d like to at least discard the first one, since I tend to prefer an object-oriented approach rather than an arbitrary function not tied to either the Mover or Attractor class. Whether you pick option 2 or option 3 is the difference between saying, “The attractor attracts the mover” and “The mover is attracted to the attractor.” Option 4 is really my favorite, though. I spent a lot of time working out the applyForce() method, and I think the examples are clearer continuing with the same technique of using this method to apply the forces.
In other words, where I once wrote
let force = createVector(0, 0.1);
mover.applyForce(force);
Made-up force
I now have this:
let force = attractor.attract(mover);
Attraction force between two objects
mover.applyForce(force);
And so the draw() function can be written as shown here:
function draw() {
background(255);
let force = attractor.attract(mover);
mover.applyForce(force);
Calculate the attraction force and apply it.
mover.update();
attractor.show();
mover.show();
}
I’m almost there. Since I decided to put the attract() method inside the Attractor class, I still need to actually write that method. It should receive a Mover object and return a p5.Vector:
attract(m) {
return ______________;
All the math
}
What goes inside the method? All of that nice math for gravitational attraction!
attract(mover) {
let force = p5.Vector.sub(this.position, mover.position);
What’s the force’s direction?
let distance = force.mag();
let strength = (this.mass * mover.mass) / (distance * distance);
force.setMag(strength);
Calculate the strength of the attraction force.
return force;
Return the force so it can be applied!
}
And I’m done. Sort of. Almost. I need to work out one small kink. Look at the code for the attract() method again. See that slash symbol for division? Whenever you have one of those, you should ask yourself this question: What would happen if the distance happened to be a really, really small number, or (even worse!) 0? You can’t divide a number by 0, and if you were to divide a number by something tiny like 0.0001, that’s the equivalent of multiplying that number by 10,000! That may be a viable outcome of this formula for gravitational attraction in the real world, but p5.js isn’t the real world. In the p5.js world, the mover could end up being very, very close to the attractor, and the resulting force could be so strong that the mover flies way off the canvas.
Conversely, what if the mover were to be, say, 500 pixels from the attractor (not unreasonable in p5.js)? You’re squaring the distance, so this will result in dividing the force by 250,000. That force might end up being so weak that it’s almost as if it’s not applied at all.
To avoid both extremes, it’s practical to constrain the range of distance before feeding it into the formula. Maybe, no matter where the Mover actually is, you should never consider it to be less than 5 pixels or more than 25 pixels away from the attractor, for the purposes of calculating the force of gravitational attraction:
distance = constrain(distance, 5, 25);
Here the constrain() function limits the value of distance between a minimum (5) and maximum (25).
Ultimately, it’s up to you to choose the behaviors you want from your simulation. But if you decide you want a reasonable-looking attraction that’s never absurdly weak or strong, constraining the distance is a good technique.
The Mover class hasn’t changed at all, so let’s just look at the main sketch and the Attractor class as a whole, adding a variable G for the universal gravitational constant. (On the book’s website, you’ll find that this example also has code that allows you to move the Attractor object with the mouse.)
Example 2.6: Attraction
let mover;
let attractor;
A mover and an attractor
let G = 1.0;
A gravitational constant (for global scaling)
function setup() {
createCanvas(640, 240);
mover = new Mover(300, 50, 2);
attractor = new Attractor();
}
function draw() {
background(255);
let force = attractor.attract(mover);
mover.applyForce(force);
Apply the attraction force from the attractor on the mover.
mover.update();
attractor.show();
mover.show();
}
class Attractor {
constructor() {
this.position = createVector(width / 2, height / 2);
this.mass = 20;
}
attract(mover) {
let force = p5.Vector.sub(this.position, mover.position);
let distance = force.mag();
distance = constrain(distance, 5, 25);
Remember, you need to constrain the distance so your circle doesn’t spin out of control.
let strength = (G * this.mass * mover.mass) / (distance * distance);
force.setMag(strength);
return force;
}
show() {
stroke(0);
fill(175, 200);
circle(this.position.x, this.position.y, this.mass * 2);
}
}
In this code, the diameter of the mover and attractor is scaled according to the mass of each object. However, this doesn’t accurately reflect how mass and size are related in our physical world. The area of a circle is calculated with the formula , where represents the radius (half the diameter) of the circle. (More about to come in Chapter 3!) As such, to represent an object’s mass proportionally with a circle’s area more accurately, I should really take the square root of the mass and scale that as the diameter of the circle.
Exercise 2.11
Adapt Example 2.6 to map the mass of the Attractor and Mover to the area of their respective circles:
circle(this.position.x, this.position.y, sqrt(this.mass) * 2);
You could, of course, expand the code to include one Attractor and an array of many Mover objects, just as I included an array of Mover objects in Example 2.5 previously.
Example 2.7: Attraction with Many Movers
let movers = [];
let attractor;
Now you have 10 movers!
function setup() {
createCanvas(640, 360);
for (let i = 0; i < 10; i++) {
movers[i] = new Mover(random(width), random(height), random(0.5, 3));
Each mover is initialized randomly.
}
attractor = new Attractor();
}
function draw() {
background(255);
attractor.show();
for (let i = 0; i < movers.length; i++) {
let force = attractor.attract(movers[i]);
Calculate an attraction force for each Mover object.
movers[i].applyForce(force);
movers[i].update();
movers[i].show();
}
}
This is just a small taste of what’s possible with arrays of objects. Stay tuned for a more in-depth exploration of adding and removing multiple objects from the canvas in Chapter 4, which covers particle systems.
Exercise 2.12
In Example 2.7, there’s a system (an array) of Mover objects and one Attractor object. Build an example that has systems of both movers and attractors. What if you make the attractors invisible? Can you create a pattern/design from the trails of objects moving around attractors?
Exercise 2.13
This chapter isn’t suggesting that every good p5.js simulation needs to involve gravitational attraction. Rather, you should be thinking creatively about how to design your own rules to drive the behavior of objects, using my approach to simulating gravitational attraction as a model. For example, what happens if you design an attractive force that gets weaker as the objects get closer, and stronger as the objects get farther apart? Or what if you design your attractor to attract faraway objects but repel close ones?
The n-Body Problem
I started exploring gravitational attraction with a simple scenario, one object attracts another object, then moved on to the slightly more complex one object attracts many objects. A logical next step is to explore what happens when many objects attract many objects!
To begin, while having separate Mover and Attractor classes has been helpful so far, this distinction is a bit misleading. After all, according to Newton’s third law, all forces occur in pairs: if an attractor attracts a mover, then that mover should also attract the attractor. Instead of two classes here, what I really want is a single type of thing—called, for example, a Body—with every body attracting every other body.
The scenario I’m describing is commonly referred to as the n-body problem. It involves solving for the motion of a group of objects that interact via gravitational forces. The two-body problem is a famously solved problem, meaning the motions can be precisely computed with mathematical equations when only two bodies are involved. However, adding one more body turns the two-body problem into a three-body problem, and suddenly no formal solution exists (see Figure 2.10).
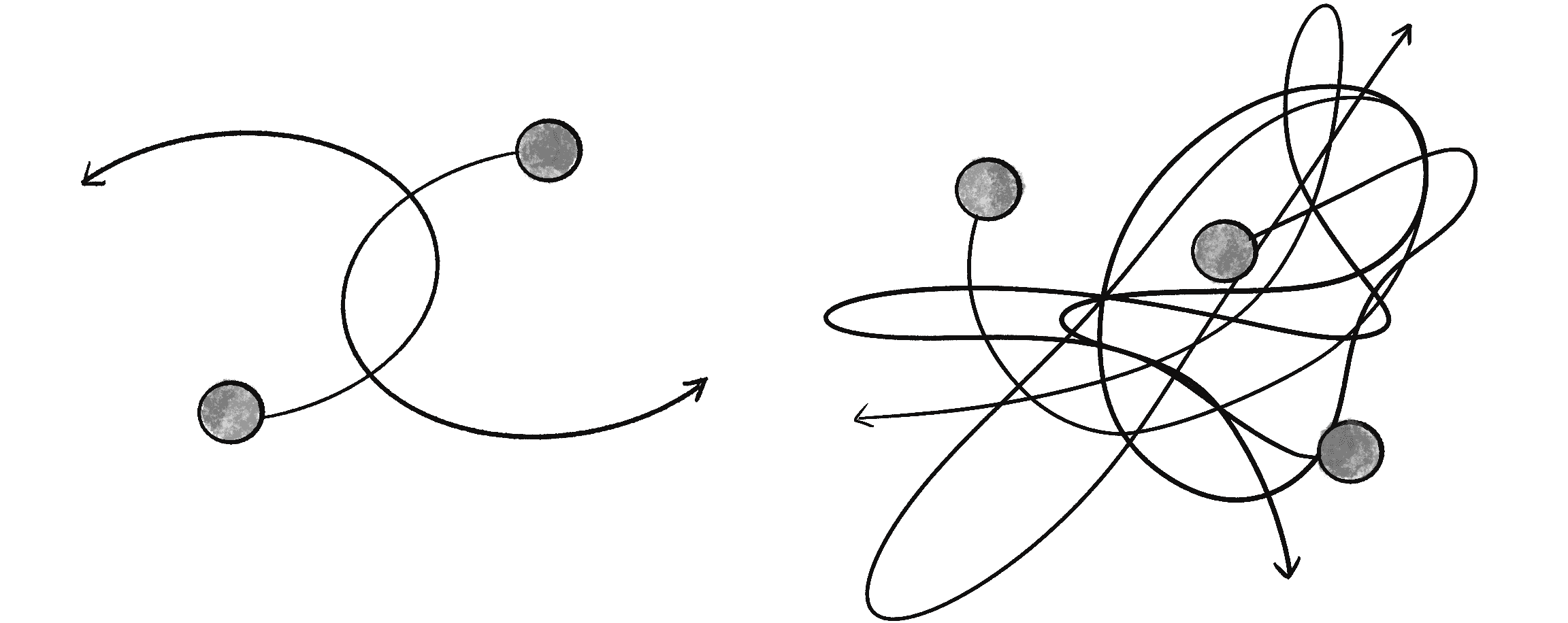
Although less accurate than using precise equations of motion, the examples built in this chapter can model both the two-body and three-body problems. To begin, I’ll move the attract() method from the Attractor class into the Mover class (which I will now call Body):
class Body {
The mover is now called a body.
/* All the other stuff from before */
attract(body) {
let force = p5.Vector.sub(this.position, body.position);
let d = constrain(force.mag(), 5, 25);
let strength = (G * (this.mass * body.mass)) / (d * d);
force.setMag(strength);
body.applyForce(force);
}
The attract() method is now part of the Body class.
}
Now it’s just a matter of creating two Body objects (let’s call them bodyA and bodyB) and ensuring that they both attract each other:
let bodyA;
let bodyB;
function setup() {
createCanvas(640, 240);
bodyA = new Body(320, 40);
bodyB = new Body(320, 200);
Create two Body objects, A and B.
}
function draw() {
background(255);
bodyA.attract(bodyB);
bodyB.attract(bodyA);
A attracts B, and B attracts A.
bodyA.update();
bodyA.show();
bodyB.update();
bodyB.show();
}
For any n-body problem, the resulting motion and patterns are entirely dependent on the initial conditions. For example, if I were to assign specific velocity vectors for each body in setup(), one pointing to the right and one pointing to the left, the result is a circular orbit.
Example 2.8: Two-Body Attraction
function setup() {
createCanvas(640, 240);
bodyA = new Body(320, 40);
bodyB = new Body(320, 200);
bodyA.velocity = createVector(1, 0);
bodyB.velocity = createVector(-1, 0);
Assign horizontal velocities (in opposite directions) to each body.
}
Example 2.8 could be improved by refactoring the code to include constructor arguments that assign the body velocities. For now, however, this approach serves as a quick way to experiment with patterns based on various initial positions and velocities.
Exercise 2.14
The paper “Classification of Symmetry Groups for Planar n-Body Choreographies” by James Montaldi and Katrina Steckles explores choreographic solutions to the n-body problem (defined as periodic motions of bodies following one another at regular intervals). Educator and artist Dan Gries created an interactive demonstration of these choreographies. Try adding a third (or more!) body to Example 2.8 and experiment with setting initial positions and velocities. What choreographies can you achieve?
I’m now ready to move on to an example with n bodies by incorporating an array:
let bodies = [];
Start with an empty array.
function setup() {
createCanvas(640, 240);
for (let i = 0; i < 10; i++) {
bodies[i] = new Body(random(width), random(height));
}
Fill the array with Body objects.
}
function draw() {
background(255);
for (let i = 0; i < bodies.length; i++) {
bodies[i].update();
bodies[i].show();
}
Iterate over the array to update and show all bodies.
}
The draw() function is where I need to work some magic so that every body exerts a gravitational force on every other body. Right now, the code reads, “For every body i, update and draw.” To attract every other body j with each body i, I need to nest a second loop and adjust the code to say, “For every body i, attract every other body j (and update and draw).”
for (let i = 0; i < bodies.length; i++) {
for (let j = 0; j < bodies.length; j++) {
For every body, check every body!
let force = bodies[j].attract(bodies[i]);
movers[i].applyForce(force);
}
movers[i].update();
movers[i].show();
}
The code has one small problem, though. When every body i attracts every body j, what happens when i equals j? Should body index 3 attract body index 3? The answer, of course, is no. If you have five bodies, you want body index 3 to attract only bodies 0, 1, 2, and 4, skipping itself. I’ll account for this by adding a conditional statement to skip applying the force when i equals j.
Example 2.9: n Bodies
let bodies = [];
function setup() {
createCanvas(640, 240);
for (let i = 0; i < 10; i++) {
bodies[i] = new Body(random(width), random(height), random(0.1, 2));
}
}
function draw() {
background(255);
for (let i = 0; i < bodies.length; i++) {
for (let j = 0; j < bodies.length; j++) {
if (i !== j) {
Do not attract yourself!
let force = bodies[j].attract(bodies[i]);
bodies[i].applyForce(force);
}
}
bodies[i].update();
bodies[i].show();
}
}
The nested loop solution in Example 2.9 leads to what’s called an n-squared algorithm, meaning the number of calculations is equal to the number of bodies squared. If I were to increase the number of bodies, the simulation would start to slow significantly because of the number of calculations required.
In Chapter 5, I’ll explore strategies for optimizing sketches like this one, with a particular focus on spatial subdivision algorithms. Spatial subdivision, in combination with the concept of quadtrees and an algorithm called Barnes-Hut, is particularly effective for improving efficiency in simulations such as the n-body one discussed here.
Exercise 2.15
Change the attraction force in Example 2.9 to a repulsion force. Can you create an example in which all the Body objects are attracted to the mouse but repel one another? Think about how you need to balance the relative strength of the forces and how to most effectively use distance in your force calculations.
Exercise 2.16
Can you arrange the bodies of the n-body simulation to orbit the center of the canvas in a pattern that resembles a spiral galaxy? You may need to include an additional large body in the center to hold everything together. A solution is offered in my “Mutual Attraction” video in the Nature of Code series on the Coding Train website.
The Ecosystem Project
Incorporate forces into your ecosystem. How might other environmental factors (for example, water versus mud, or the current of a river) affect the way a character moves through an ecosystem?
Try introducing other elements into the environment (food, a predator) for the creature to interact with. Does the creature experience attraction or repulsion to things in its world? Can you think more abstractly and design forces based on the creature’s desires or goals?
 CODING TRAIN
CODING TRAIN




